Помогите пожалуйста :(((((

Ответы
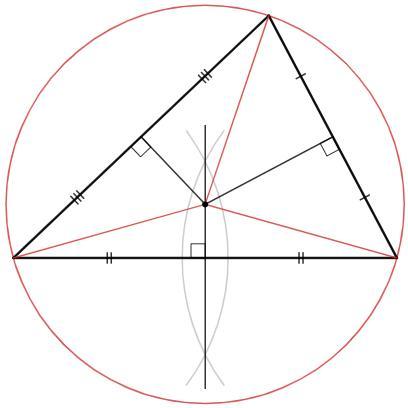
1) Проведем две дуги одинакового радиуса (больше половины отрезка) с центрами в концах отрезка. Прямая через точки пересечения дуг - серединный перпендикуляр к отрезку.
Любая точка серединного перпендикуляра равноудалена от концов отрезка. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке - эта точка равноудалена от вершин и является центром описанной окружности треугольника.
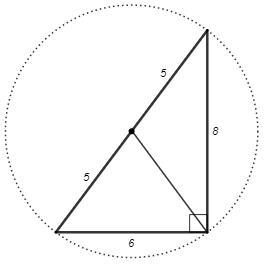
2) Медиана из прямого угла равна половине гипотенузы. Следовательно середина гипотенузы равноудалена от вершин и является центром описанной окружности. Радиус описанной окружности равен половине гипотенузы.
Гипотенуза по теореме Пифагора.
с =√(6^2 +8^2) =10 (м)
R =c/2 =5 (м)
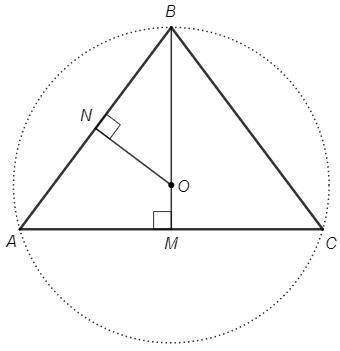
3) M, N - середины сторон. Медиана BM к основанию равнобедренного треугольника является также высотой, то есть серединным перпендикуляром.
Проведем серединный перпендикуляр к боковой стороне (через N). Пересечение серединных перпендикуляров - центр описанной окружности O.
В сантиметрах
AM =AC/2 =6
BN =AB/2 =5
BM =√(AB^2 -AM^2) =8 (т. Пифагора)
△ABM~△OBN (прямоугольные, ABM - общий)
AB/OB =BM/BN => OB =10*5/8 =6,25 (см)