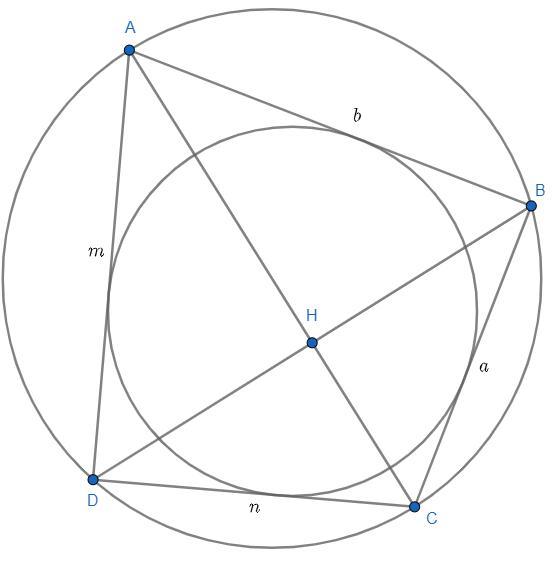
Четырёхугольник ABCD вписан в окружность, причём диаметром
окружности является его диагональ AC . Также известно, что в ABCD
можно вписать окружность.
а) Докажите, что отрезки AC и BD перпендикулярны.
б) Найдите радиус вписанной окружности четырёхугольника ABCD , если
AC = 26 и BD =10.
Срочно.
Ответы
Ответ:
а) Доказано; б) .
Объяснение:
а)
Пусть AB=b, BC=a, DC=n, AD=m.
Понятно, что ΔADC и ΔABC прямоугольные (AC - диаметр окружности по условию)
Из теоремы Пифагора и условия вписанности окружности в четырехугольник следует:
Рассмотрим вторую строку системы:
Выполним сложение первой строки исходной системы и полученной:
Теперь заметим, что из 2-ой строки исходной системы .
Тогда:
Соответственно и .
Значит ΔDBC и ΔDAB равнобедренные.
Пусть в ΔDAB ∠DAO=α и ∠BAO=β. Тогда ∠ADB=90°-β, а ∠ABD=90°-α.
Но ∠ADB=∠ABD => α=β. Значит AO - биссектриса ∠DAB, а => и высота (ΔDAB равнобедренный) => AC⊥BD.
Доказано!
б)
Понятно, что искать радиус будем, записав формулу площади исходного четырехугольника двумя способами, т.е:
Здесь в 1-ой формуле sin90°=1.
По теореме Пифагора:
Но высота треугольника DAC:
Тогда:
Итого:
Задание выполнено!