Предмет: Математика,
автор: kanatovamad
Вычислите предел функции
Приложения:
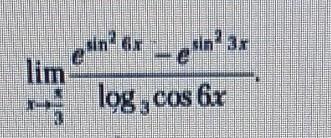
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Использован переход к эквивалентным бесконечно малым функциям.
Пусть - БМФ при
. Тогда:
Похожие вопросы
Предмет: Другие предметы,
автор: IgorSlim
Предмет: Русский язык,
автор: dasha162002dubr
Предмет: Русский язык,
автор: vorobevajuli
Предмет: Литература,
автор: machkalyanlaura
Предмет: Литература,
автор: светлана406