Question

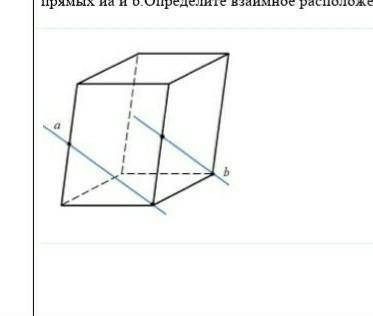
Точки А и В – середины ребер параллелепипеда. Определите взаимное расположение прямых иa и b.Определите взаимное расположение прямых a и b.​

Answer 1

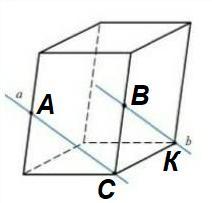
Не совсем понятно, как проходят прямые, через середины рёбер А и В - понятно, а проходят ли они через вершины параллелепипеда - в условии ничего не сказано.

Предположим, что прямая $a$ проходит через точку А и вершину параллелепипеда С, то есть прямая $a$ лежит в плоскости, содержащей  переднюю грань параллелепипеда (ABC).

Предположим, что прямая $b$ проходит через точку B и вершину параллелепипеда K, то есть прямая $b$ лежит в плоскости, содержащей правую боковую грань параллелепипеда (BCK).

Тогда прямые $a$ и $b$ скрещиваются, так как прямая $a$ лежит в плоскости (АВС), а прямая $b$ пересекает эту плоскость в точке В, не принадлежащей прямой $a$.

$B\in b;\ \ K\in b\ \ \Rightarrow\ \ b\subset (BCK)\\\\A\in a;\ \ C\in a\ \ \Rightarrow\ \ a\subset (ABC);\\ \\ B\in (ABC);\ \ B\notin a\ \ \ \Rightarrow\ \ \ a\ \dot {-}\ b$

Ответ: прямые скрещиваются.