Предмет: Математика,
автор: garalushaplay
Помогите пожалуйста решить иррациональные уравнения
Приложения:
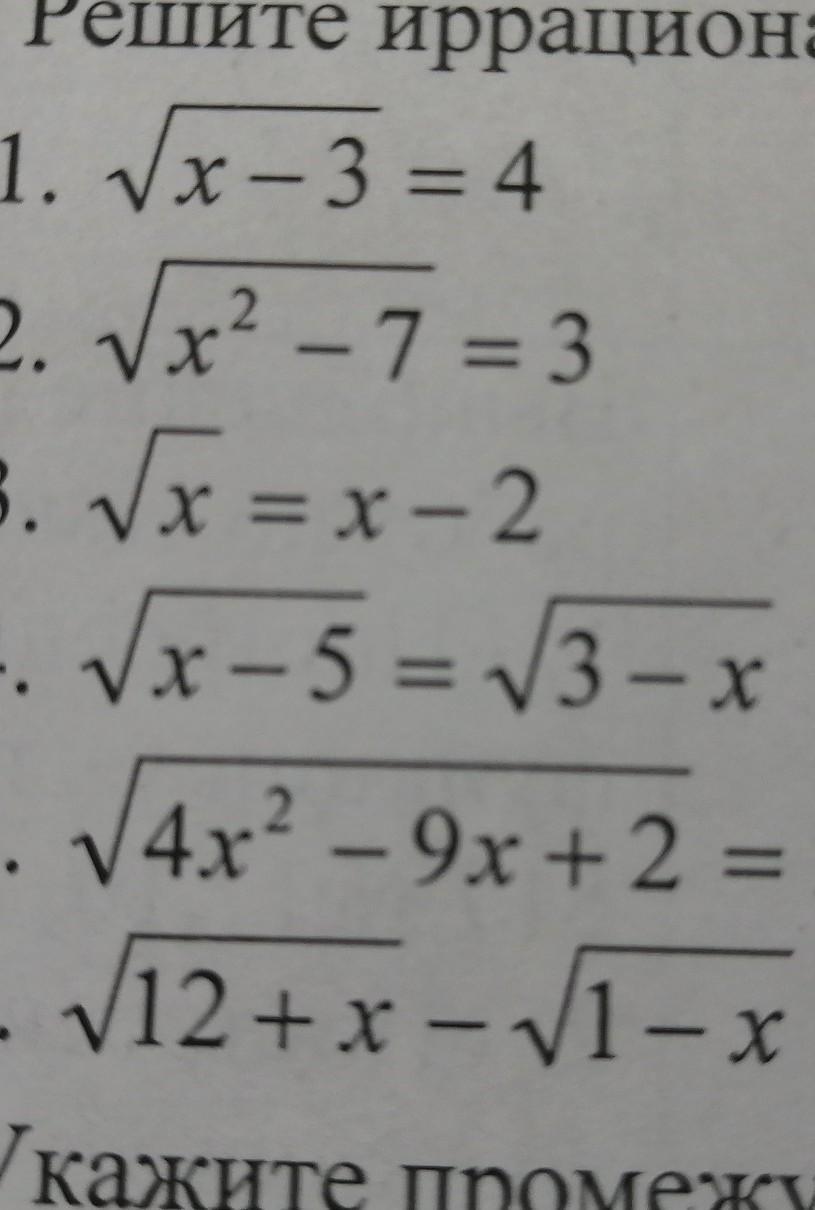
Ответы
Автор ответа:
1
Ответ:
1) x=19
2) x₁ = -4; x₂ = 4
3) x = 4
4) Решений нет.
5) и 6) условия не полные.
Пошаговое объяснение:
1)
Проверка:
2)
3)
Проверка.
. x = 1 не является решением.
. Верно. Уравнение имеет 1 корень x=4.
4)
Проверка:
Корень четной степени из отрицательного числа не существует. Уравнение не имеет решений.
Похожие вопросы
Предмет: Русский язык,
автор: shmaxim
Предмет: Другие предметы,
автор: yaroslavvolkov0
Предмет: Английский язык,
автор: tcherepenkovaa
Предмет: Алгебра,
автор: stebaevadi2004
Предмет: Математика,
автор: alugd