Question

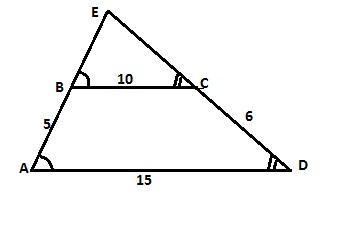
продолжения боковых сторон ab и cd трапеции abcd пересекаются в точке e.найдите площадь треугольника aed,если ab=5 см,bc=10 см,cd=6 см,ad=15 см​

Answer 1

Ответ:

S = 108 cм².

Объяснение:

В трапеции сторона ВС параллельна AD. Следовательно, треугольники ВЕС и АЕD подобны.

Коэффициент подобия равен k= BC/AD = 10/15 = 2/3.

Из подобия имеем:

ВЕ/(5+ВЕ) = 2/3. =>  BE = 10см  => AE = АВ+ВЕ = 5+10 = 15см.

ЕС/(6+ЕС) = 2/3. => EC = 12 см. => ED = CD+EC = 6+12 = 18см.

По формуле Герона найдем площадь треугольника АЕD:

S = √(p·(p-a)(p-b)(p-c)), где a, b и с - стороны, р - полупериметр.

р = 24 => S = √(24·9·9·6) = 9·6·2 = 108 cм².