Question

Мальчик переплывает реку и плывёт (относительно воды) со
скоростью в два раза меньше скорости течения реки. Под
каким углом фк направлению течения реки он должен
плыть, чтобы его снесло течением как можно меньше? На
какое расстояние S его снесёт в этом случае, если ширина
реки L = 100 м? Угол ф вырази в градусах, путь ѕ
метрах, округлив результаты до целых значений.​

Answer 1

Ответ:

60°

173 м

Объяснение:

Задача олимпиадная.

Дублирую свое более раннее решение.

Обозначим скорость мальчика относительно воды за v₁, а скорость течения реки, за v₂, тогда скорость мальчика относительно берега (по закону сложения скоростей):

$\displaystyle \vec{v}=\vec{v_1}+\vec{v_2}$

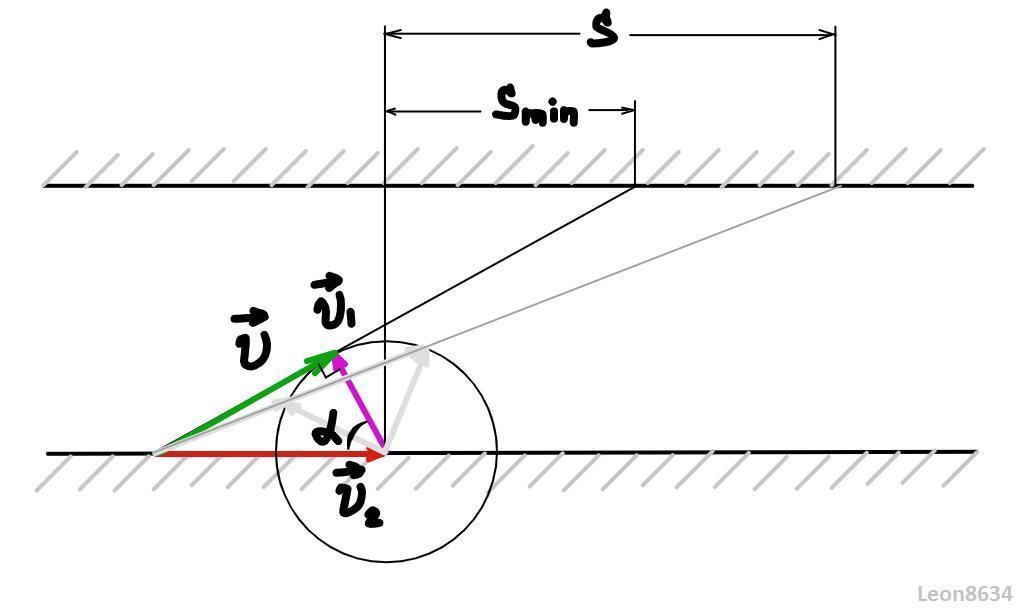
Скорость течения реки v₂ жестко фиксирована в пространстве, а скорость мальчика, оставаясь неизменной по модулю, может менять свой угол относительно берега.Таким образом, конец вектора скорости мальчика описывает некоторую окружность (см. рисунок). Расстояние, на которое мальчика снесет по течению реки к моменту, когда он достигнет противоположного берега, равно длине отрезка, ограниченного начальным положением мальчика и точкой пересечения прямой, содержащей вектор результирующей скорости с противоположным берегом. Из геометрических соображений ясно, что длина этого отрезка минимальна при максимально возможном угле между векторами v₁ и v₂, это соответствует случаю, когда вектор результирующей скорости направлен по касательной к окружности. Из образовавшегося прямоугольного треугольника легко найти искомый угол:

$\displaystyle \alpha =arccos(\frac{v_1}{v_2} )=arccos(0.5)=60^0$

Путь найдем из геометрических соображений:

$\displaystyle s=Ltg\alpha=100*tg60^0=100\sqrt{3}=173$ м.