Question

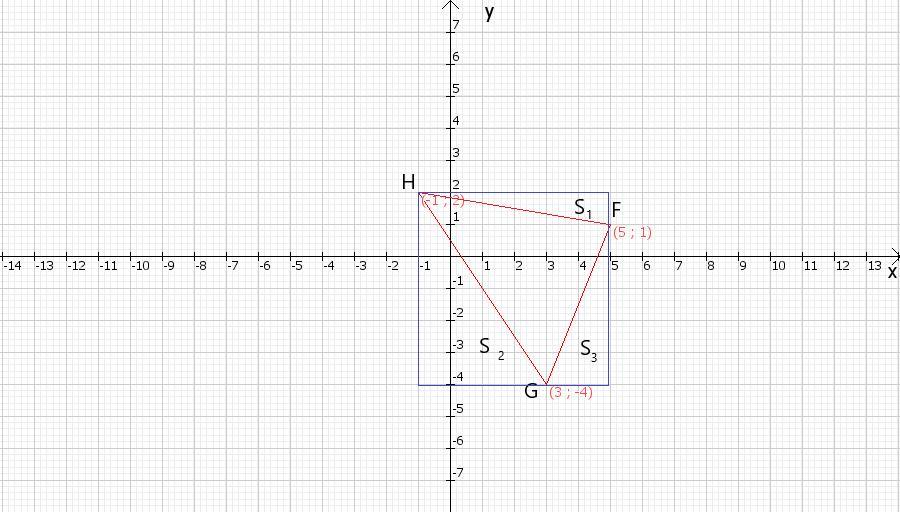
77. Начертите треугольник, вершины которого находятся в точках F(5; 1),
G(3;-4), Н(-1; 2), и вычислите его площадь.​

Answer 1

Ответ:

Площадь треугольника составляет 16 кв. ед.

Объяснение:

ДАНО: треугольник с вершинами F(5; 1), G(3;-4), Н(-1; 2)

НАЙТИ: S - ?

Опишем вокруг треугольника квадрат. Сторона квадрата равна 6 единиц. Площадь квадрата состоит из заданного квадрата и еще трех прямоугольных треугольников.

Найдем площади этих прямоугольных треугольников по формуле $\displaystyle S=\frac{1}{2} ab$, где  a,b - катеты.

По графику определяем длину катетов.

$\displaystyle S_1=\frac{1}{2}* 6*1=3$ (кв. ед)

$\displaystyle S_2=\frac{1}{2}* 6*4=12$ (кв. ед)

$\displaystyle S_3=\frac{1}{2}* 5*2=5$ (кв. ед)

Площадь квадрата вычисляется по формуле S₀ = a².

S₀ = 6² = 36 (кв. ед)

Тогда искомая площадь треугольника найдем как разность площадей квадрата и прямоугольных треугольников.

S = S₀ - (S₁ + S₂ + S₃) = 36 - (3 + 12 + 5) = 36 - 20 = 16 (кв. ед)