Предмет: Геометрия,
автор: Violetta6367
Дан параллелограмм, вершины которого лежат на одной окружности. Найди его периметр, если соотношение сторон этого параллелограмма 10:24, а радиус окружности — 65 см.
Ответы
Автор ответа:
8
Ответ:
340 см
Объяснение:
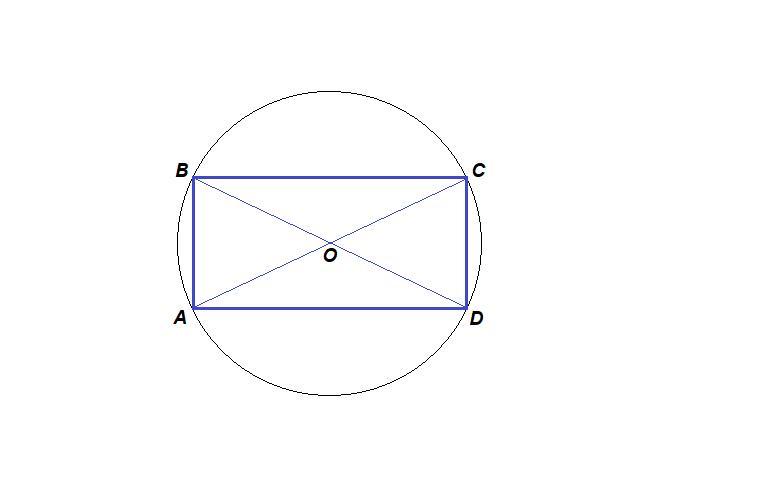
Сумма противоположных углов вписанного четырехугольника равна 180°. Противоположные углы параллелограмма равны. Тогда
∠А = ∠С = 180° : 2 = 90°
Значит, это прямоугольник.
Центр окружности, описанной около прямоугольника лежит в точке пересечения диагоналей.
Значит, диагональ - диаметр окружности.
АС = 2 · 65 = 130 см
АВ : ВС = 10 : 24
Пусть х - коэффициент пропорциональности,
АВ = 10х, ВС = 24х.
Из прямоугольного треугольника АВС по теореме Пифагора составим уравнение:
(10x)² + (24x)² = 130²
100x² + 576x² = 16900
676x² = 16900
x² = 25
x = 5 или x = - 5 - не подходит по смыслу задачи.
АВ = 10 · 5 = 50 см
ВС = 24 · 5 = 120 см
Периметр прямоугольника:
P = 2(AB + BC) = 2(50 + 120) = 2 · 170 = 340 см
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Kristinhik
Предмет: Русский язык,
автор: annakovaljova83
Предмет: Русский язык,
автор: evzavjalova
Предмет: Алгебра,
автор: Аноним
Предмет: Алгебра,
автор: xtentacion