сравните значение выражение 10²⁰ и 20¹⁰
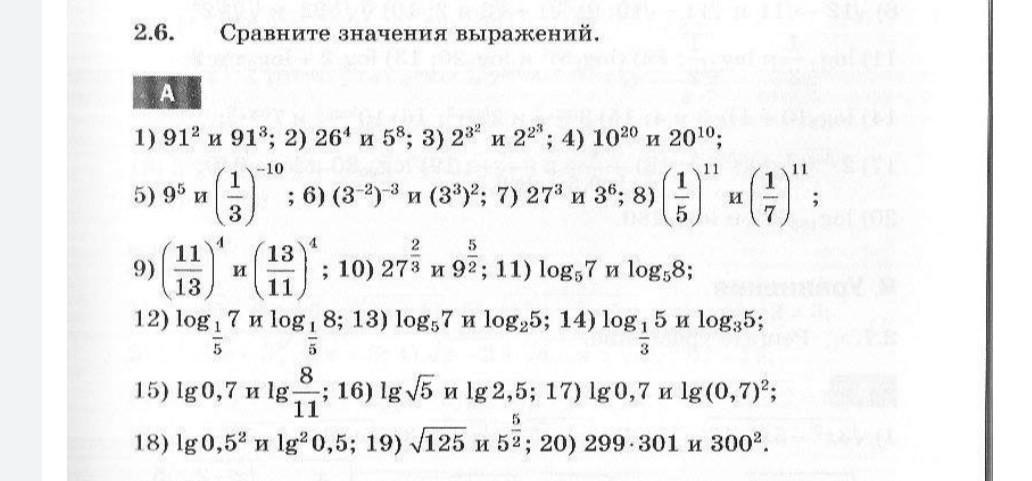
Ответы
Ответ:
Пошаговое объяснение:
Ответ:
Пошаговое объяснение:
1. 91² и 91³; основание степени одинаково, значит больше то число, у которого больше показатель
91³>91².
2. 26⁴ и 5⁸;
5⁸=(5²)⁴=25⁴;
26⁴>25⁴; показатели одинаковы, различные основания, больше число с большим основанием
3. 2^(3^2) 2^(2^3); сначала действия со степенями (в скобках)
3²=9; 2³=8
2^(3^2)=3²=9;
2^(2^3)=2³=8;
2^(3^2)>2^(2^3)
4. 10²⁰ 20¹⁰;
20¹⁰=(2*10)¹⁰=2¹⁰*10¹⁰; учтем, что 2¹⁰=1024≈10³;
20¹⁰≈10³*10¹⁰≈10¹³;
10²⁰ >10¹³ ⇔ 10²⁰ > 20¹⁰
5. 9⁵ (1/3)⁻¹⁰;
(1/3)⁻¹⁰=1/(3⁻¹⁰)=3¹⁰=(3²)⁵=9⁵; они равны!
9⁵ = (1/3)⁻¹⁰.
6. (3⁻²)⁻³ (3³)²;
(3⁻²)⁻³=3⁽⁻²°⁽⁻³⁾⁾=3⁺⁶;
(3³)²=3³°²=3⁶; они равны!
(3⁻²)⁻³ = (3³)²;
7. 27³ 3⁶
27³=(3³)³=3⁹;
27³ > 3⁶.
8. (1/5)¹¹ (1/7)¹¹; показатели одинаковы, различные основания, больше число с большим основанием
1/5>1/7
(1/5)¹¹ > (1/7)¹¹.
9. (11/13)⁴ (13/11)⁴; показатели одинаковы, различные основания, больше число с большим основанием
11/13<13/11 (т.к. 13/11 >1, а 11/13<1)
(11/13)⁴ < (13/11)⁴
10. 27^(2/3) 9^(5/2)
27^(2/3)=(3^3)^(2/3)=3²;
9^(5/2)=(3^2)^(5/2)=3⁵;
3⁵>3² ⇔27^(2/3) < 9^(5/2)
11. log₅7 log₅8; основание логарифма одинаковы и больше 1.
log₅7 < log₅8
12.log ₁₎₅7 log₁₎₅8; основание логарифма одинаковы и меньше 1.
log ₁₎₅7 > log₁₎₅8
Все, времени больше нет ((