Предмет: Математика,
автор: sidorovitnastya
Здравствуйте. Помогите решить. Желательно с объяснением. номер 8
Приложения:
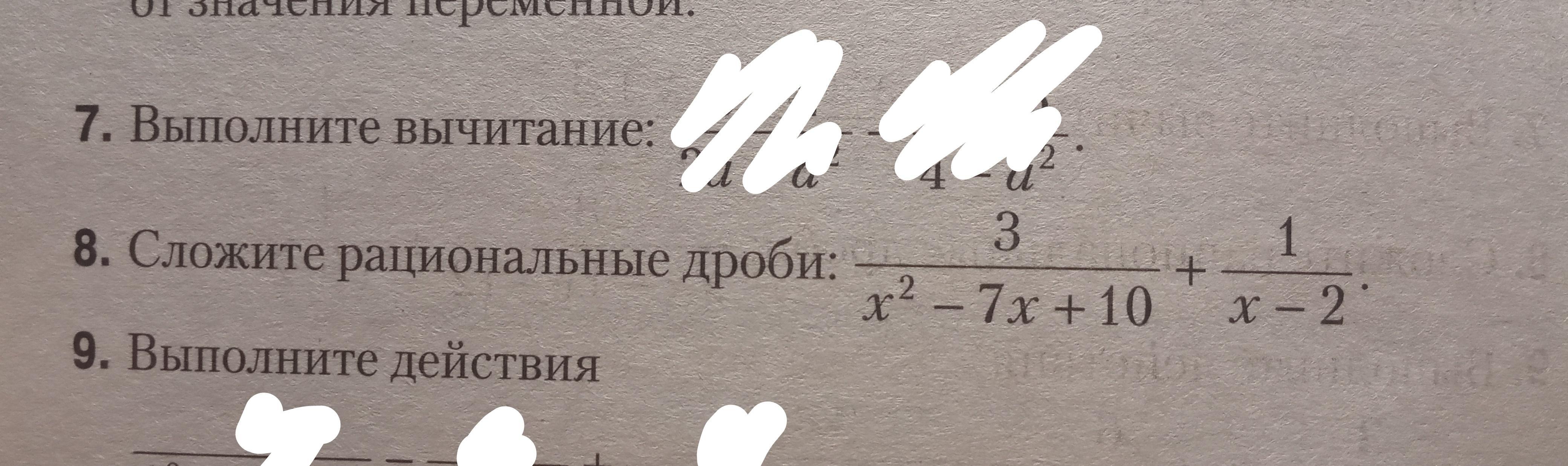
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
В знаменателе первой дроби содержится квадратный трёхчлен. Разложим его.
Решим это уравнение по теореме Виета:
Подставим полученное произведение в знаменатель первой дроби:
Для того, чтобы привести обе дроби к общему знаменателю, умножим числитель и знаменатель второй дроби на x-5:
Похожие вопросы
Предмет: Русский язык,
автор: Kiril2139
Предмет: Английский язык,
автор: irairairavas
Предмет: Русский язык,
автор: Аноним
Предмет: Информатика,
автор: Zpok