Предмет: Геометрия,
автор: Kthf99
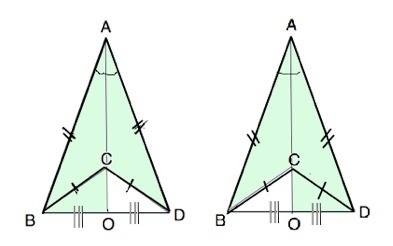
Диагональ АС невыпуклого четырехугольника АВСD, в котором АВ=АD>ВС=СD,разделяет его на 2 треугольника. Прямые АС и ВD пересекаются в точке О. Сравните периметры пятиугольников ВСОDА и DСОВА.
Если можно с чертежем.
Ответы
Автор ответа:
0
Рассмотрим треугольники ВАС и DAC. Они равны по трем сторонам - две по условию, АС - общая Следовательно, ∠ВАС=∠DAC.
В ∆ ВАD боковые стороны равны, углы при вершина А прямой АО делятся пополам ( из доказанного выше), следовательно, ∆ ВАD равнобедренный и АО его биссектриса и медиана.
∆ ВСО=∆ DCО по трем сторонам.
Периметры пятиугольников АВОСD и АВСОD –сумма равных отрезков. Следовательно, они равны.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: primachenkoalina
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Математика,
автор: vasilisalebedeva0810
Предмет: Математика,
автор: lisich2002
Предмет: Математика,
автор: egor1337