Предмет: Алгебра,
автор: Аноним
Алгебра))))))))))))))
Приложения:
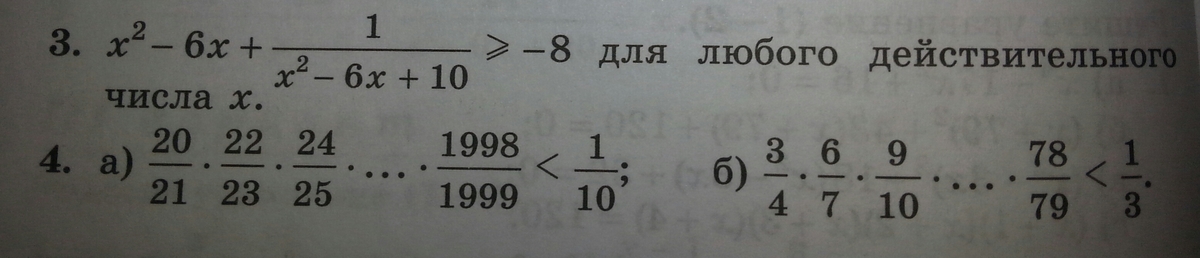
Ответы
Автор ответа:
0
3)
дальше замену делать не надо , так как квадрат всегда больше или равен 0
4) Сделаем так, докажем неравенство более сильное, что бы лучше понять , у вас дана 5<8, я хочу доказать 5<6 (что то вроде такого)

докажем теперь более сильно по сравнению этой , неравенство вида

ее можно так же записать как
 , теперь перейдем к нашей, но более строгой чем последняя
, теперь перейдем к нашей, но более строгой чем последняя

теперь очевидно что
 так как числитель больше знаменателя , значит мы можем зафиксировать значение ,дадим ему приоритет средний
так как числитель больше знаменателя , значит мы можем зафиксировать значение ,дадим ему приоритет средний  тогда
тогда

верно, значит и наше выражение справедливо, так как мы доказали более сильное A1⇔A2
3)
так как знаменатель больше числителя то , то справедливо неравенство

при подстановке получим

то есть мы уже предположили что знаменатель этой дроби равен 3^26*78 , что ложно, и доказательство идет уже с погрешностью иными словами мы перешли от более слабого к сильному
дальше замену делать не надо , так как квадрат всегда больше или равен 0
4) Сделаем так, докажем неравенство более сильное, что бы лучше понять , у вас дана 5<8, я хочу доказать 5<6 (что то вроде такого)
докажем теперь более сильно по сравнению этой , неравенство вида
ее можно так же записать как
теперь очевидно что
верно, значит и наше выражение справедливо, так как мы доказали более сильное A1⇔A2
3)
так как знаменатель больше числителя то , то справедливо неравенство
при подстановке получим
то есть мы уже предположили что знаменатель этой дроби равен 3^26*78 , что ложно, и доказательство идет уже с погрешностью иными словами мы перешли от более слабого к сильному
Похожие вопросы
Предмет: Русский язык,
автор: atorutaev2010
Предмет: Русский язык,
автор: mariacherepko
Предмет: Химия,
автор: Аноним
Предмет: Литература,
автор: Аноним
Предмет: Математика,
автор: 56754