Предмет: Математика,
автор: nikitafox36
Найдите производную функции: y=(lnx)^3^x
NNNLLL54:
условие уточните: y=((lnx)^3)^x или y=(lnx)^{3^x} ?
Ответы
Автор ответа:
1
Ответ:
решение на фотографии
Приложения:
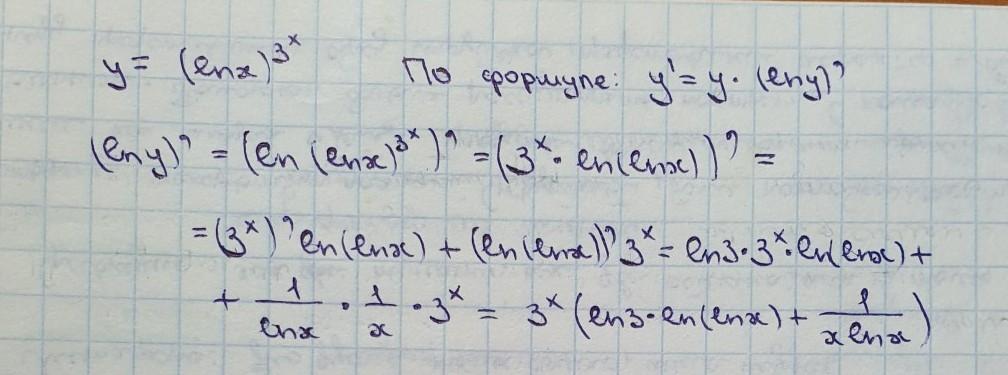
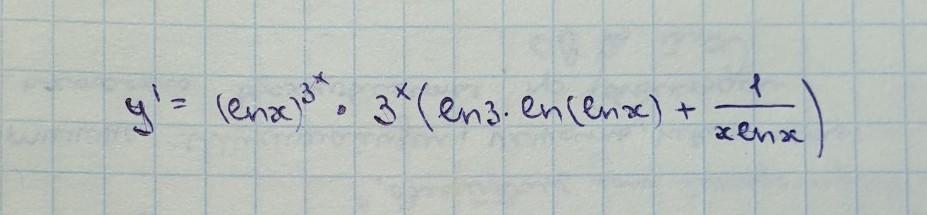
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: Samalaxmetova
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: агент09
Предмет: Литература,
автор: Kissule4ka
Предмет: Алгебра,
автор: Игорь1999999