Предмет: Геометрия,
автор: leragorodilina
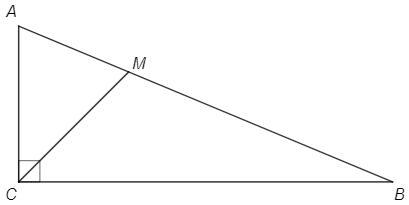
Биссектриса, проведенная из вершины С прямого угла треугольника АВС,
пересекается с гипотенузой ВС в точке М . Bычислитe площадь треугольника
АМС ,если катеты данного треугольника АС=5 см, СВ= 12 см
Ответы
Автор ответа:
1
S(ABC) =1/2 AC*BC =5*12/2 =30 (см^2)
AM/MB =AC/BC =5/12 (теорема о биссектрисе)
AM=5x, MB=12x => AB =5x+12x =17x
S(AMC)/S(ABC) =AM/AB =5/17 (площади треугольников с равной высотой относятся как основания)
S(AMC) =30*5/17 =150/17 (см^2) ~8,82
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: msolga0510
Предмет: Русский язык,
автор: vadimzaseev
Предмет: Другие предметы,
автор: radionova05
Предмет: Математика,
автор: Tёma20070212
Предмет: Математика,
автор: arinahachuknigu