Question

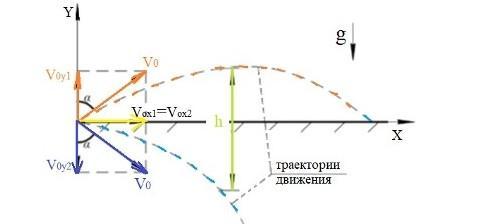
На некоторой высоте из одной точки одновременно бросили два шара: один вверх, а другой вниз, оба со скоростью 40 м/с и под углом 600 к горизонту. На каком расстоянии друг от друга будут находиться шары через 2 секунды?
помогите прям очень надо,чтобы кто-то решил эту задачу ​

Answer 1

Ответ:

80 м

Объяснение:

Так как горизонтальные проекции их начальных скоростей одинаковы, то мысленный отрезок, их соединяющий, все время будет оставаться вертикальным и расстояние между шарами совпадет с разностью их вертикальных координат:

$\displaystyle \Delta=y_1(t)-y_2(t)$

Распишем уравнения их движения вдоль вертикальной оси:

$\displaystyle y_1(t)=v_0cos\alpha t -\frac{gt^2}{2}$

$\displaystyle y_2(t)=-v_0cos\alpha t -\frac{gt^2}{2}$

Расстояние между ними:

$\displaystyle \Delta=v_0cos\alpha t-\frac{gt^2}{2}+v_0cos\alpha t+\frac{gt^2}{2}=2v_0cos\alpha t=2*40*cos(60^0)*2=80$ м.

Примечание: судя по рисунку шары брошены под углом 60° к вертикальной оси, а не к горизонту, если нет то альтернативный ответ 139 м.