Предмет: Алгебра,
автор: Аноним
помогите пожалуйста
Приложения:
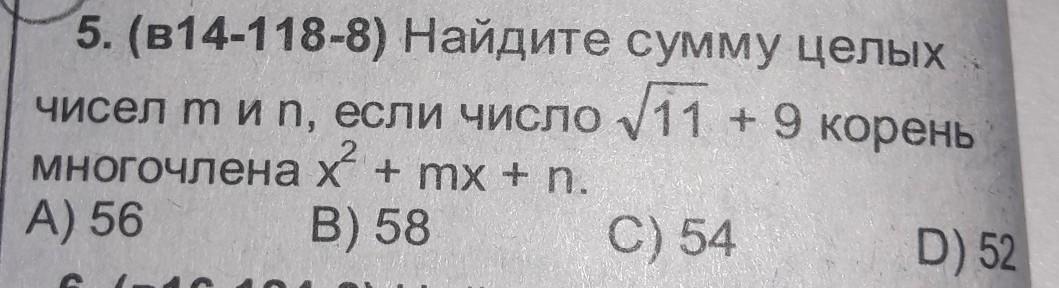
Ответы
Автор ответа:
1
Поскольку m и n - целые числа, справа в этом равенстве стоит целое число. Если бы 18+m не равнялось нулю, мы имели бы равенство
откуда следовало бы, что
является рациональным числом, что не соответствует действительности. Поэтому 18+m=0; m= - 18.
Остается найти n из равенства 92+9m+n=0; n= - 92 +162=70; m+n=52.
Ответ: D
Замечание. Иррациональность числа доказывается стандартным способом: если предположить, что
где дробь справа можно считать несократимой, то
откуда
делится на 11, а тогда и a делится на 11, то есть a=11c;
откуда следует, что
делится на 11, а тогда и b делится на 11, что противоречит несократимости дроби a/b.
Похожие вопросы
Предмет: Русский язык,
автор: ololoshazlat
Предмет: Русский язык,
автор: valeriy1997
Предмет: Русский язык,
автор: Помощнина
Предмет: Алгебра,
автор: LyubaKo8
Предмет: Геометрия,
автор: UtkinaVioletta