Предмет: Геометрия,
автор: dianaginiatulina
Вокруг равностороннего треугольника описана окружность радиуса 3√3.
Найдите радиус вписанной окружности.
Можно с рисунком и ришением.
Ответы
Автор ответа:
3
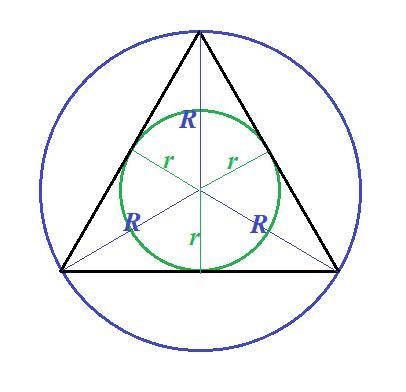
В равностороннем треугольнике биссектрисы являются одновременно и высотами, и медианами. Поэтому центры вписанной и описанной окружностей совпадают с точкой пересечения медиан, которые делятся точкой пересечения в отношении 2 к 1, считая от вершин.
Для равностороннего треугольника радиус описанной окружности R в два раза больше радиуса вписанной окружности r:
По условию радиус описанной окружности , тогда радиус вписанной окружности:
Ответ: 1,5√3
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Mashenka15200205
Предмет: Українська мова,
автор: KurtNirvana
Предмет: Другие предметы,
автор: katyachup
Предмет: Математика,
автор: малышка92
Предмет: Математика,
автор: ksd2004