Предмет: Алгебра,
автор: xasex8
Вычислите интегралы, преобразуя подынтегральные функции
Приложения:
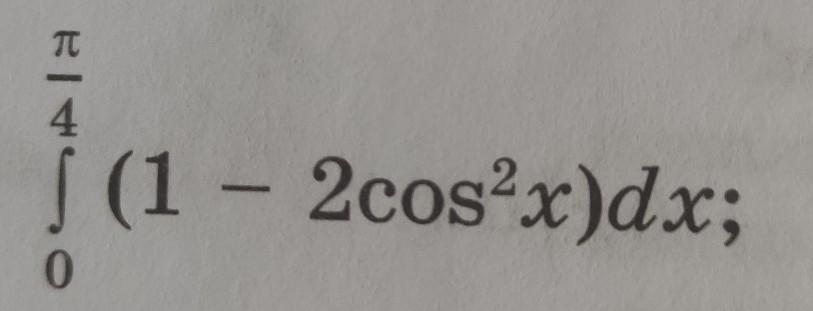
Ответы
Автор ответа:
1
Объяснение:
Автор ответа:
1
Ответ:
Примечание. Использованные формулы:
— косинус двойного угла
— формула Ньютона—Лейбница (здесь
— первообразная функции
)
— метод введения под знак дифференциала
Похожие вопросы
Предмет: Русский язык,
автор: wwwsilhouete
Предмет: Русский язык,
автор: alisa031203
Предмет: Русский язык,
автор: pro100filia
Предмет: Геометрия,
автор: annadihtyar05