Предмет: Геометрия,
автор: влада220602
Дана прямоугольная трапеция, у которой длинная сторона а и острый угол a, в нее вписана ОКРУЖНОСТЬ. Найди площадь трапеции
siestarjoki:
если ф острый угол, то S= a^2 *tg(ф/2)
по сути, задача на разрезание
биссектриса острого угла делит такую трапецию пополам
Ответы
Автор ответа:
1
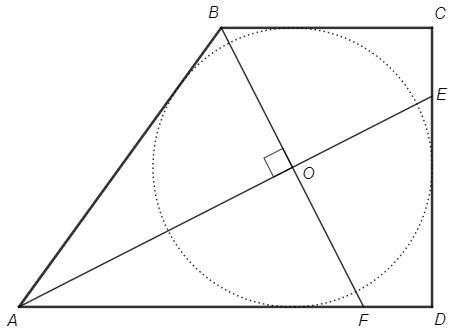
AE, BF - биссектрисы
∠AOB=90 (угол между биссектрисами внутренних углов при параллельных)
Биссектриса AO является высотой, следовательно и медианой, BO=OF.
В четырехугольнике OBCE сумма противоположных углов 180 =>
∠OBC =180-∠OEC =∠OED
OBCE=OEDF (по трем углам и двум смежным сторонам)
S(ABCE) =S(ABO)+S(OBCE) =S(AFO)+S(OEDF) =S(AED)
ED =AD tg(A/2)
S(AED) =1/2 AD^2 tg(A/2)
S(ABCD) =2 S(AED) =AD^2 tg(A/2)
Приложения:
Решение неполное.
Для равенства четырехугольников надо доказать OB=OE=OF
Проведем радиусы в точки касания L, M, N (на BC, CD, AD соответственно). ∠FON=∠BOL=90-∠LOE=∠EOM. Треугольники равны по катету и острому углу - гипотенузы равны.
Похожие вопросы
Предмет: Русский язык,
автор: kolova01
Предмет: Другие предметы,
автор: superlerka15
Предмет: Русский язык,
автор: Mark0oKor
Предмет: Алгебра,
автор: Whithoutme