Предмет: Алгебра,
автор: Аноним
РЕШИТЕ ПОЖАЛУЙСТА С ГРАФИКОМ!30 БАЛЛОВ!
Приложения:
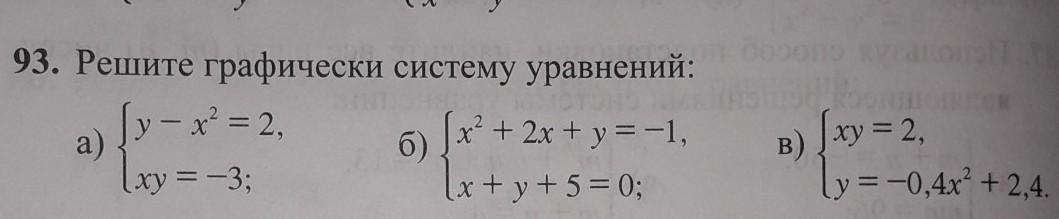
Ответы
Автор ответа:
0
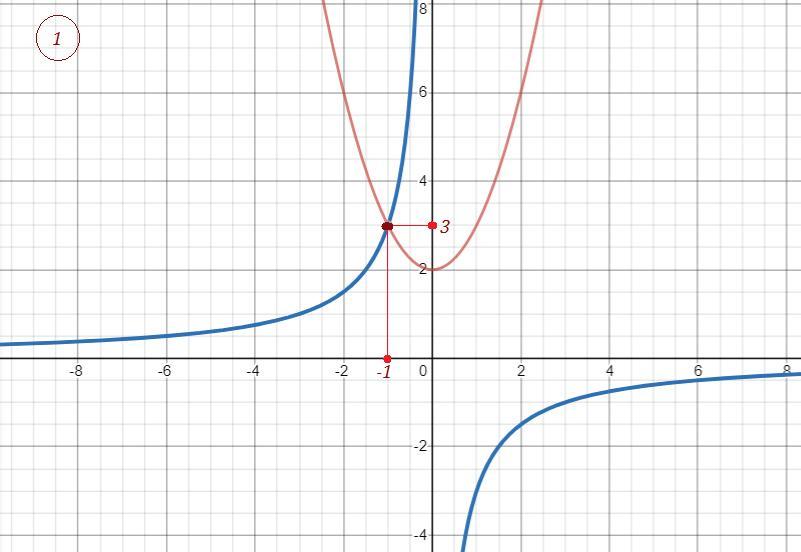
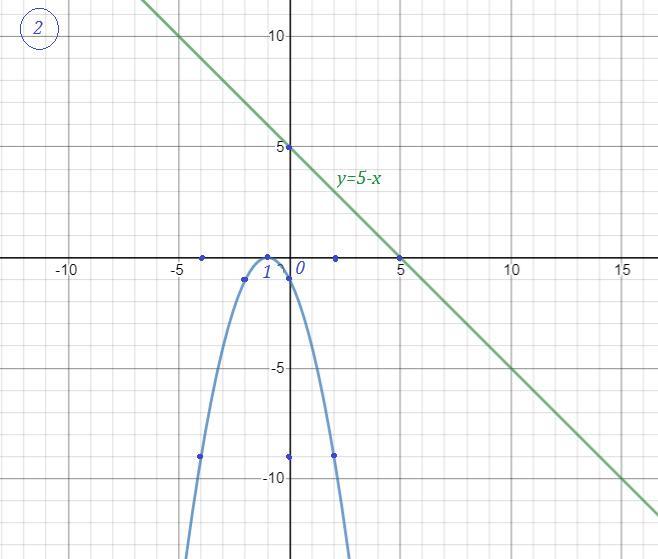
Парабола и прямая не пересекаются, значит решений нет .
Приложения:
Похожие вопросы
Предмет: Українська література,
автор: nadiaslatina
Предмет: Русский язык,
автор: vdfuuu
Предмет: Русский язык,
автор: annazo2001
Предмет: Математика,
автор: krsk16