Предмет: Математика,
автор: Ffufufghg
помогите решить 1 замечательный придел
Приложения:
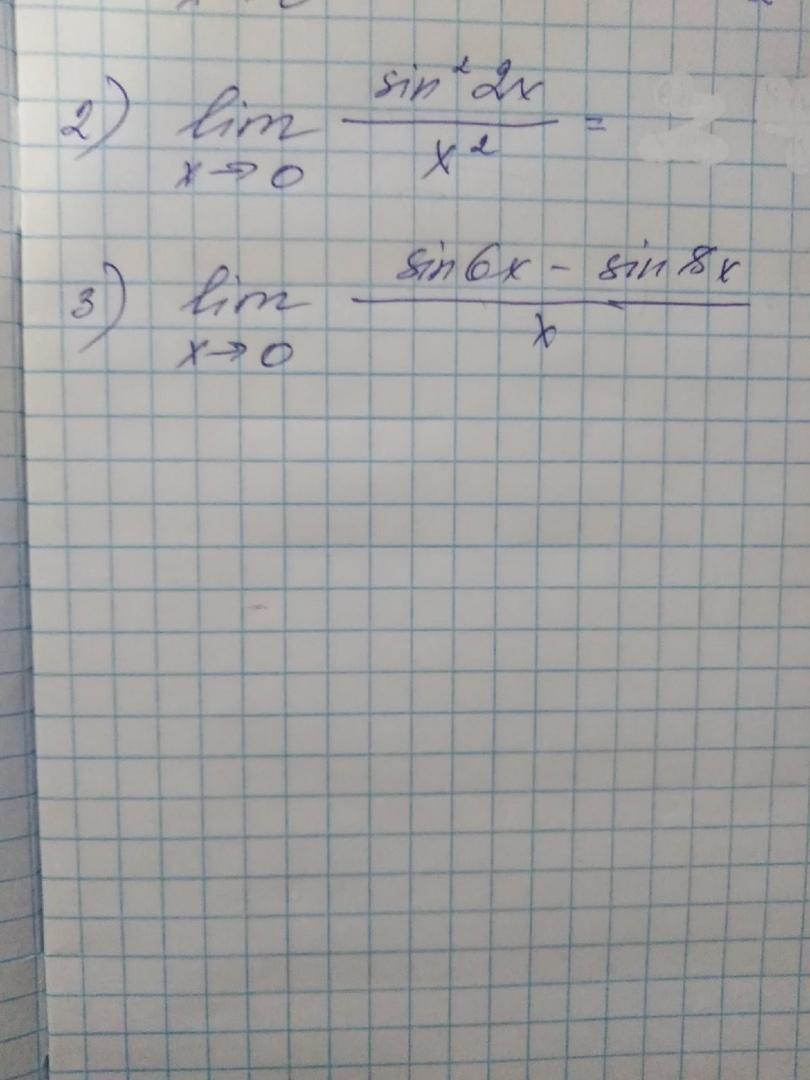
Ответы
Автор ответа:
1
Ответ:
4
-2
Пошаговое объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: катяяякр
Предмет: Русский язык,
автор: annabeauty2004
Предмет: Английский язык,
автор: Galinka23
Предмет: Математика,
автор: radomskayad8084