Предмет: Алгебра,
автор: brawljeki
помогите пожалуйста
Приложения:
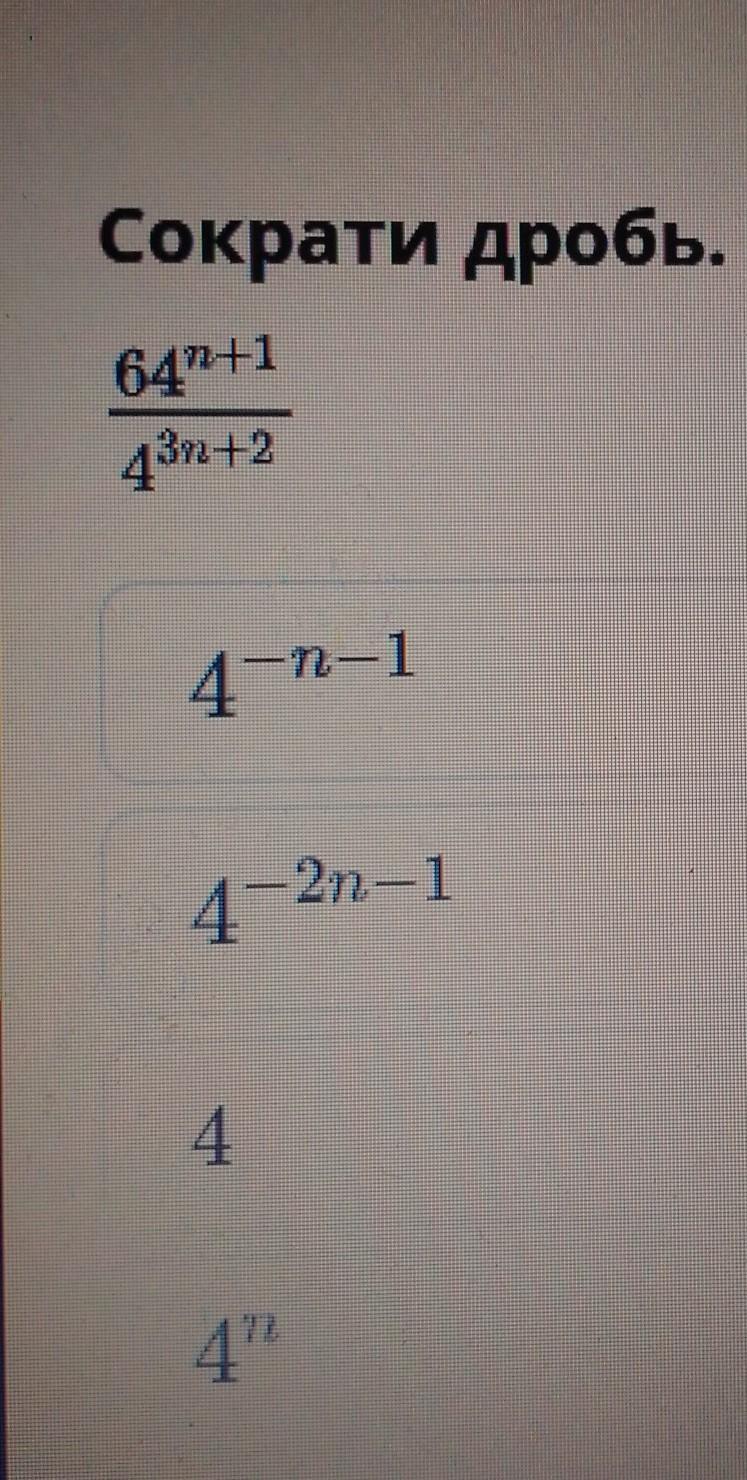
Ответы
Автор ответа:
0
Ответ:
3)
Объяснение:
Можно так:
Или так:
Похожие вопросы
Предмет: Русский язык,
автор: cherkasovaoks
Предмет: Русский язык,
автор: Prilukovka007
Предмет: Українська мова,
автор: шеймус5234
Предмет: Физика,
автор: Doninov1990