Предмет: Алгебра,
автор: sanek0703
ООООЧЕЕЕНЬ СРООООЧНООО
Найти точки, в которых значение производной функции f(х) равно 1
Приложения:
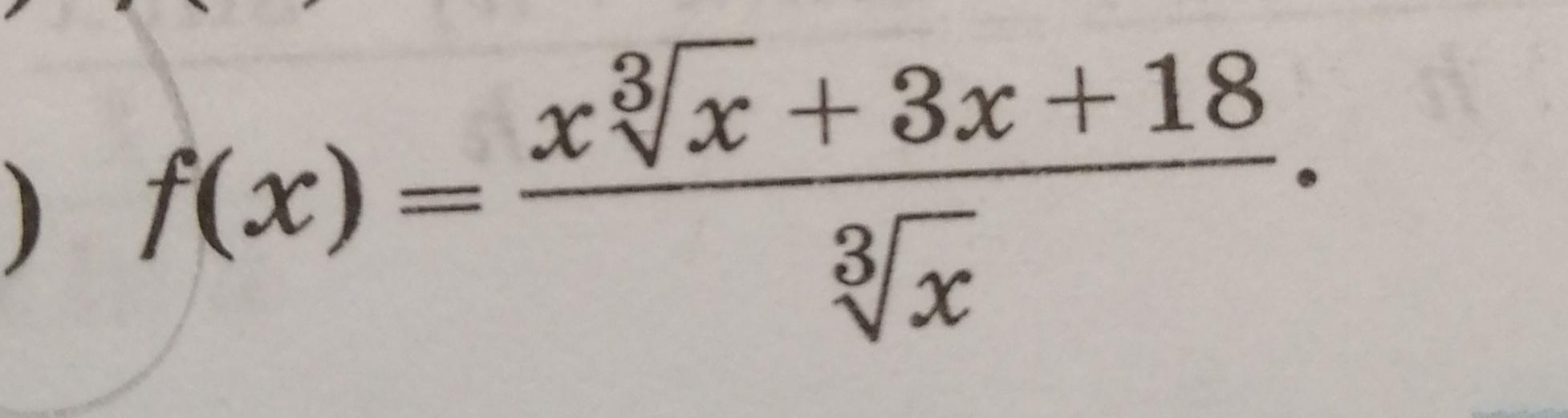
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: Lukoc
Предмет: Английский язык,
автор: nataschasmolsk
Предмет: Русский язык,
автор: elenemmi
Предмет: Литература,
автор: ВероникаСоколова1
Предмет: Математика,
автор: tweenArmagedonus