Question

Один из внешних углов прямоугольного треугольника равен 120 градусов ,найдите большую и меньшую сторону треугольника если их сумма равна 24 см

Answer 1

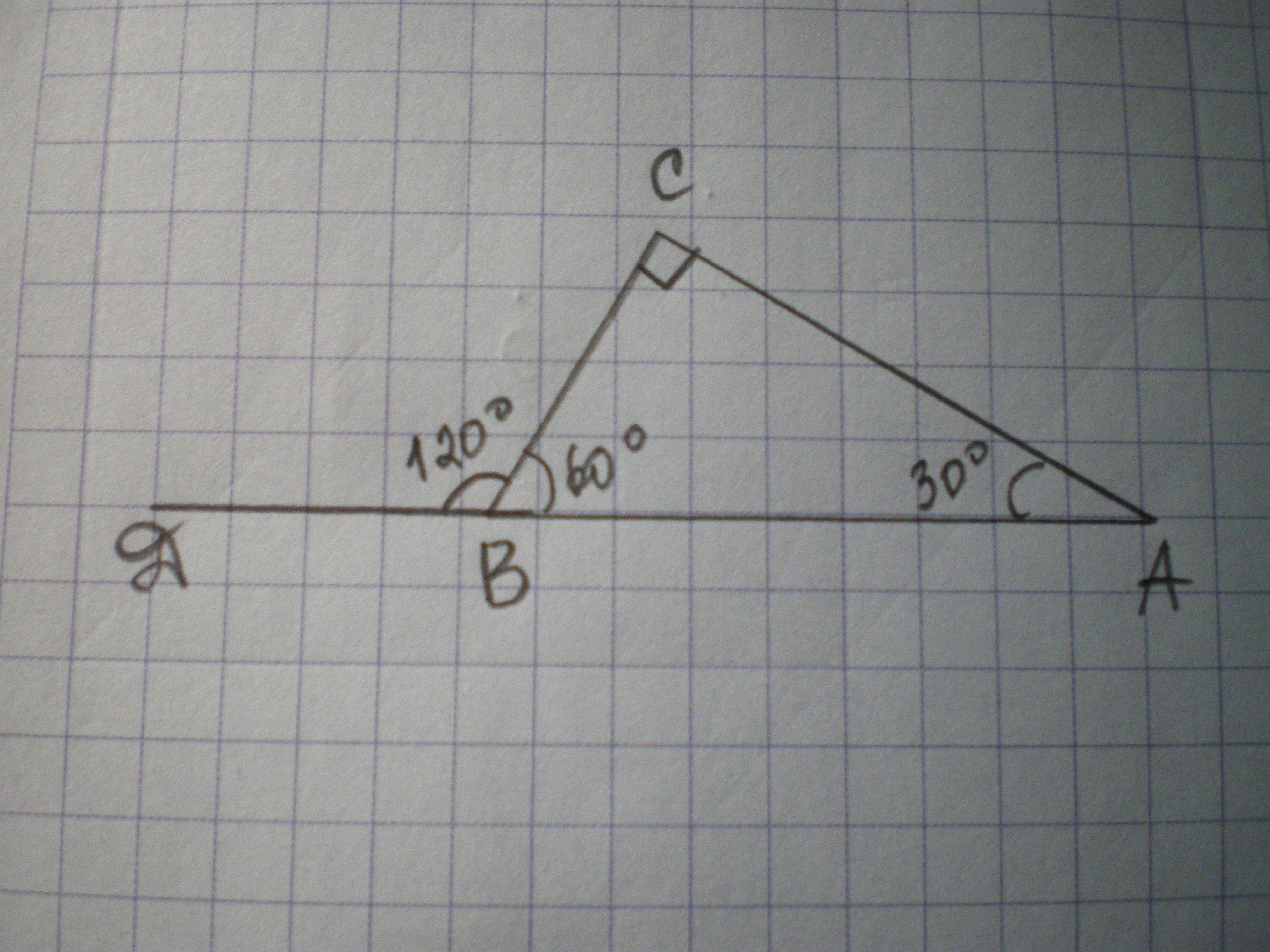
Дано: ΔАВС - прямоугольный, ∠С=90°, ∠ДВС=120°, АВ+ВС=24 см.

Найти АВ, ВС.

По свойству смежных углов ∠ДВА+∠СВА=180°, тогда

∠СВА=180-∠ДВС=180-120=60°.

По свойству острых углов прямоугольного треугольника

∠А=90-∠СВА=90-69=30°

В треугольнике против большей стороны лежит больший угол, поэтому АВ - большая сторона. Против меньшей стороны лежит меньший угол, поэтому ВС - меньшая сторона.

ВС=12 АВ по свойству катета, лежащего против угла 30°.

Составим уравнение: АВ+12 АВ = 24;  1,5 АВ = 24;  АВ=16 см.

ВС=16:2=8 см.

Ответ: 8 см, 16 см.