Предмет: Математика,
автор: sofiyakoroleva
Вычислите неопределенный интеграл методом замены:
Приложения:
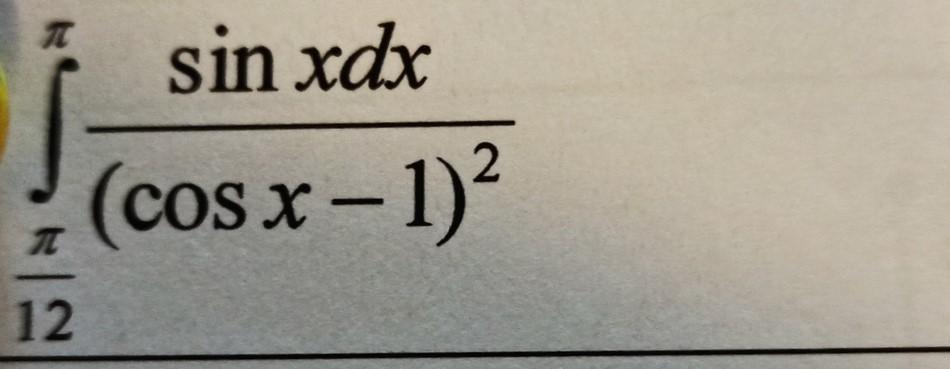
FlatEarth:
cинус под дифференциал : int(-d(cos(x))/(cos(x)-1)^2) . cos(x) = t ; int(-dt/(t-1)^2) = 1/(t-1) = 1/(cos(x)-1) , подставляйте пределы.
*=1/(cos(x)-1)
pi/12 = pi/3 -pi/4, используем формулу косинуса разности.
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Прежде чем считать сам интеграл найдем:
Теперь перейдем к самому интегралу:
Автор ответа:
0
-sinxdx=d(cosx)=d(cosx-1)
замена cosx-1=у
у верхн. =сosπ=-1-1=-2
у нижн.=сosπ/12-1
-∫y⁻²dy=1/y
подставим пределы интегрирования. получим
1/(-2)-1/(сosπ/12-1)
сosπ/12=сos(π/3-π/4)= сos(π/3)*сos(π/4)+sin(π/4)*sin(π/3)=
(1/2)*(√2/2)+(√2/2)*(√3/2)=(√2/4)(√3+1)
1/(-2)-1/(сosπ/12-1)=-1/2-1/((√2/4)(√3+1)-1)=-1/2-4/(√2+√6-4)
=(-8-√2-√6+4)/(√2+√6-4)=-(√2+√6+4)/(√2+√6-4)=(√2+√6+4)/(-√2-√6+4)=
(4+√2+√6)/(4-√2-√6)
Похожие вопросы
Предмет: Қазақ тiлi,
автор: aikorkemjetkerg
Предмет: Другие предметы,
автор: Валерончик001
Предмет: Русский язык,
автор: dan38
Предмет: География,
автор: ICinderellaI