Помогите пожалуйста сделать
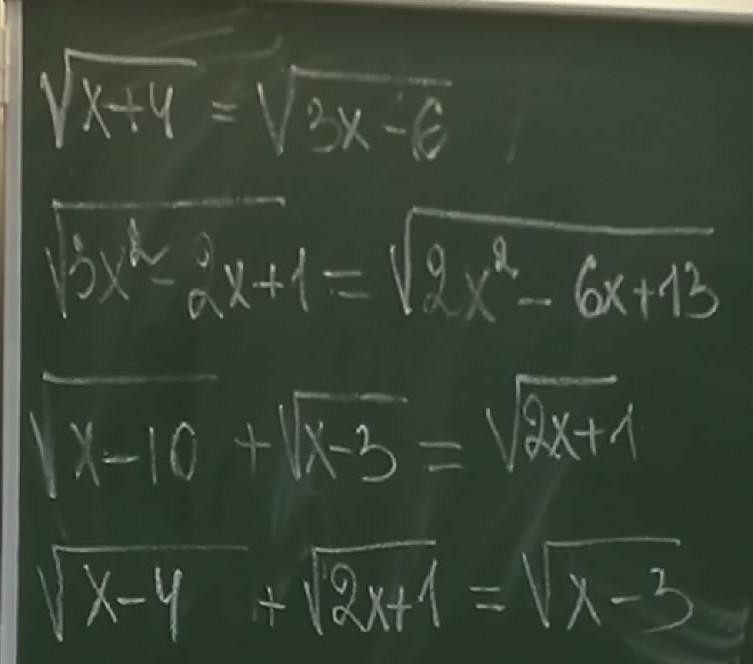
Ответы
Ответ:
Пошаговое объяснение:
√(x+4)=√(3x-6); x+4≥0; ⇒ x≥-4; 3x-6≥0; x≥2
x∈[2;+∞)
(√(x+4))²=(√(3x-6))²;
x+4=3x-6; x-3x=-6-4; -2x=-10;
2x=10; x=5
√(3x²-2x+1)=√(2x²-6x+13);
3x²-2x+1≥0; D=4-12<0; x∈(-∞;+∞)
2x²-6x+13≥0; D=36-8*13<0; x∈(-∞;+∞)
(√(3x²-2x+1))²=(√(2x²-6x+13))²;
3x²-2x+1=2x²-6x+13;
3x²-2x²-2x+6x+1-13=0;
x²+4x-12=0; D=16+48=64;
x₁₂=0,5(-4±8);
x₁=2; x₂=-6.
√(x-10)+√(x-3)=√(2x+1); √4.3+√11.3=√29.3;
x-19≥0; x≥19;
x-3≥0; x≥3;
2x+1≥0; x≥-1/2,
x∈[19;+∞)
(√(x-10)+√(x-3))²=(√(2x+1))²;
x-10+2√((x-10)(x-3))+x-3=2x+1;
2x-13-2x-1+2√(x²-3x-10x+30)=0;
-14+2√(x²-13x+30)=0;
√(x²-13x+30)=14/2;
(√(x²-13x+30))²=49;
x²-13x+30-49=0;
x²-13x-19=0; D=169+76=245=5*49;
x₁₂=0,5(13±7√5);
x₁=6,5+3,5√5
x₂=6,5-3,5√5<19 - не подходит!
x∈[19;+∞).
√(x-4)+√(2x+1)=√(x-3);
x-4≥0; x≥4;
2x+1≥0; x≥-1/2;
x-3≥0; x≥3;
x∈[4;+∞)
(√(x-4)+√(2x+1))²=(√(x-3))²;
x-4+2x+1-x+3+2√((x-4)(2x+1))=0;
2x+2√((x-4)(2x+1))=0;
x²=(-√((x-4)(2x+1)))²;
x²=2x²+x-8x-4;
x²-2x²+7x+4=0;
x²-7x-4=0; D=49+16=65
x₁₂=0,5(7±√65);
x₁=3,5+0,5√65;
x₂=3,5-0,5√65<4 не подходит!
x∈[4;+∞)
Проверяем для x₁:
√(x-4)+√(2x+1)=√(x-3); x₁=3,5+0,5√65≈7,5;
√3,5+√16≠√4,5;
Уравнение не имеет решений!