Предмет: Геометрия,
автор: DIMAOLIJINIK
ПОМОГИТЕ СРОЧНО ДАМ 20 БАЛОВ. Стороны треугольника равны 7 см, 8 см и 12 см. Данный треугольник остроугольный? (Сделает в форме задачи, с рисунком).
cos20093:
Ну сложность только в угле напротив стороны 12, ясно что два других угла острые. Чтобы понять, какой угол напротив большей стороны, можно поступить так. Если бы между сторонами 7 и 8 был прямой угол, то выполнялась бы теорема Пифагора. Тогда третья сторона (гипотенуза) в квадрате была бы равна 49+64=113. Это меньше, чем 12^2 =144; то есть напротив стороны 12 тупой угол.
Ответы
Автор ответа:
1
Воспользуемся теоремой косинусов
a² =b²+c²-2bc*cos A
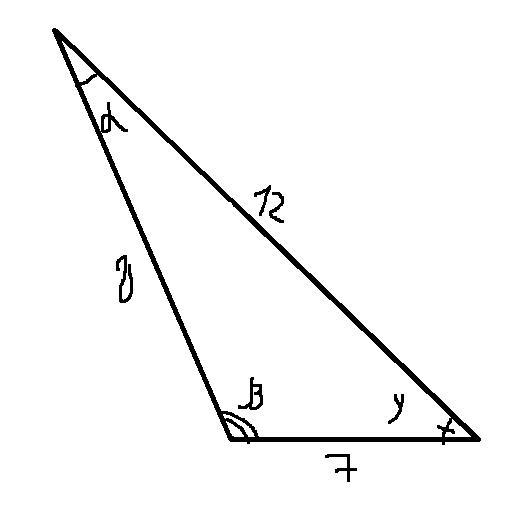
Теперь применим её к нашему треугольнику(см. вложение) :
1) 7² = 12² + 8² - 2*12*8*cos α
2*12*8*cos α = 144 + 64 - 49
192*cos α = 159
Косинус положительный ⇒ угол α острый
2) 12² = 7² + 8² - 2*7*8*cos β
2*7*8*cos β = 49 + 64 - 144
112*cos β = -31
Косинус отрицательный ⇒ угол β тупой
3) 8² = 7² + 12² - 2*7*12*сos γ
2*7*12*сos γ = 49 + 144 - 64
168*сos γ = 129
сos γ =
Косинус положительный ⇒ угол γ острый
Ответ: треугольник тупоугольный
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Vicha200
Предмет: Русский язык,
автор: vildanova19861
Предмет: Українська мова,
автор: romashka0771
Предмет: Математика,
автор: Аноним
Предмет: Физика,
автор: nersesian2000