Даю 40 баллов решите качественно
Ответы
Ответ:
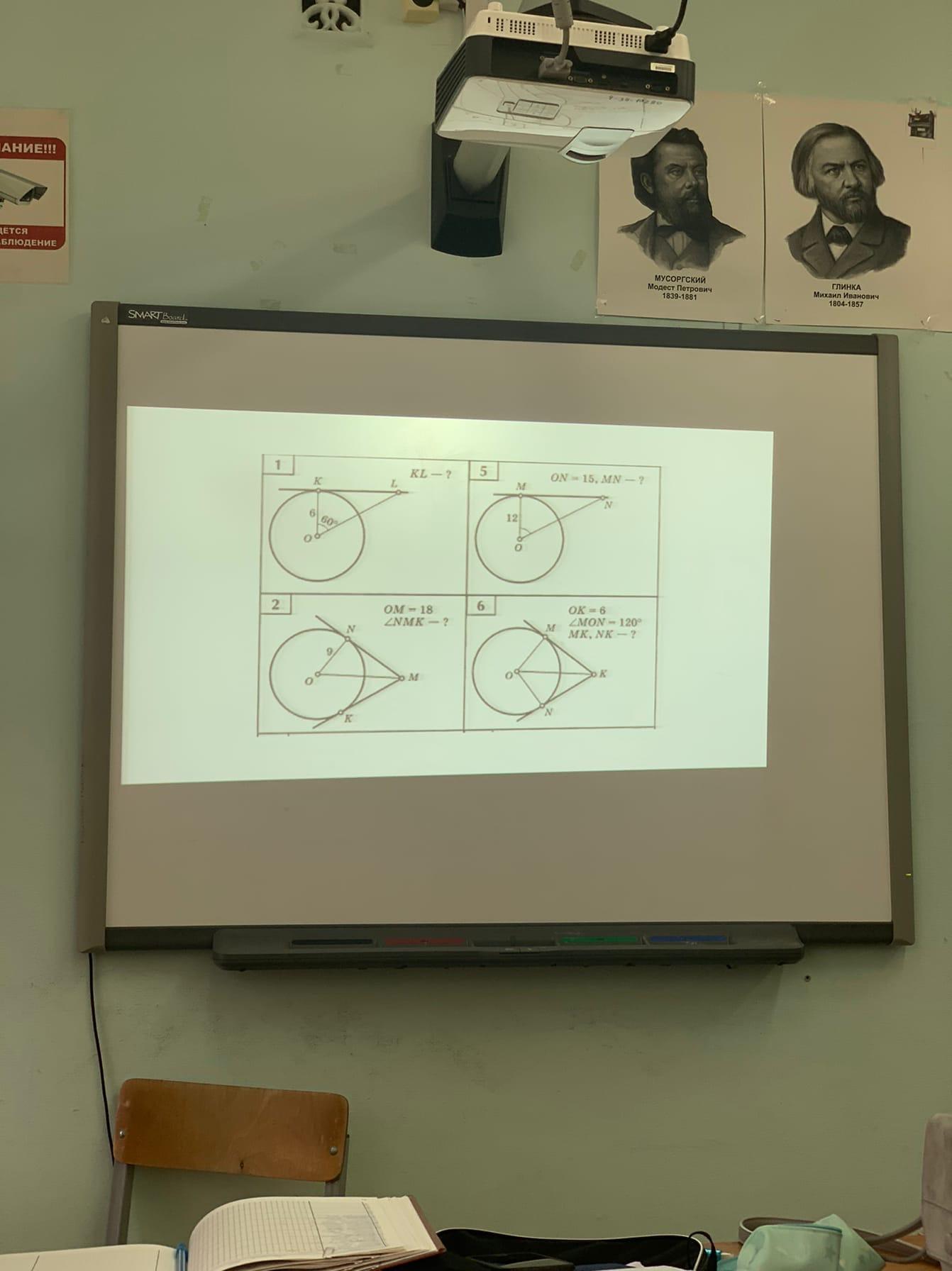
1)KL=6√3
2)NMK=60°
5)MN=9
6)MK=NK=3√3
Объяснение:
1)угол К = 90°( по свойству касательной), тогда угол L = 90°-60°= 30°, тогда ОК=1/2 ОL, а ОL= 12. По теореме Пифагора (∆ОКL прямоугольный) KL= √144 - 36 = √108 = 6√3
2)Как в первом задании угол N = 90° тогда ∆ NMO прямоугольный, а так как катет ON в два раза меньше гипотенузы ОМ, то угол NMO = 30° . Угол NMO = углу ОМК = 30°, тогда угол NMK =60 °(исходя из свойства о касательных из одного пункта за окружностью)
5)Угол М = 90° , тогда ∆ОМN прямоугольный, и по теореме обратной Пифагору МN= 9 ( Пифагоровы тройка)
6)Угол МОК=углу КОN так как ∆ МОК=∆КОN (из свойства о касательных из одного пункта).Тогда угол МОК =120°/2=60°, следовательно угол МКО = 30° (∆МОК прямоугольный ) тогда ОК = 2 ОМ, и ОМ=3. Потеореме Пифагора МК(=NK из равности треугольников) =√ 36-9 = √ 27 = 3√3
Ответ:
1) КL - касательная ⇒ KL ⊥ OK=R , ∠OLK=90°-60°=30° ,
В прямоугольном треугольнике против угла в 30° лежит катет, равный половине гипотенузы ⇒ OL=2*R=2*6=12 ,
По теореме Пифагора: KL²=OL²-OK²=144-36=108 , KL=√108=6√3 .
2) ΔOMN - прямоугольный , ON⊥ MN ,
гипотенуза MN=18 , катет ON=9 ⇒ ∠OMN=30° ,
Точка К - точка касания, тогда ∠NMK=2*∠OMN=2*30°=60°
5) ΔOMN - прямоугольный , ∠OMN=90° ,
по теореме Пифагора: MN²=ON²-OM²=15²-12²=225-144=81 ,
MN=9
6) ΔOMK=ΔONK как прямоугольные треугольники с равными катетами
OM=ON=R ) и общей гипотенузой ОК ⇒ MK=NK .
∠МОК=∠NOK=1/2*∠MON=1/2*120°=60°
∠ОКМ=90°-60°=30° ⇒ ОМ=1/2*ОК=1/2*6=3 ,
MK²=OK²-OM²=6²-3²=36-9=27 , MK=√27=3√3