Предмет: Алгебра,
автор: saidastan
неопределенный интеграл
Приложения:
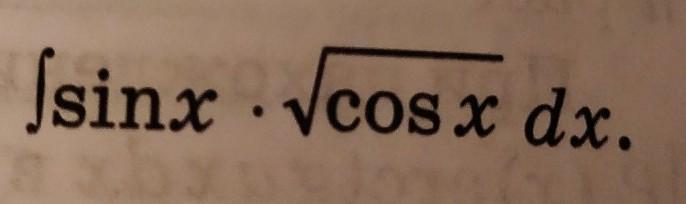
Ответы
Автор ответа:
1
Ответ:
Объяснение:
По формуле
Пусть теперь , тогда
По формуле интеграла степенной функции:
Учитывая нашу замену, запишем:
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: Ирина7788
Предмет: Русский язык,
автор: СвЕТуЛя25
Предмет: Русский язык,
автор: dianaibragimov2
Предмет: Геометрия,
автор: УмруЗаРодину