Предмет: Алгебра,
автор: livusle0
Помогите пожалуйста решить
Приложения:
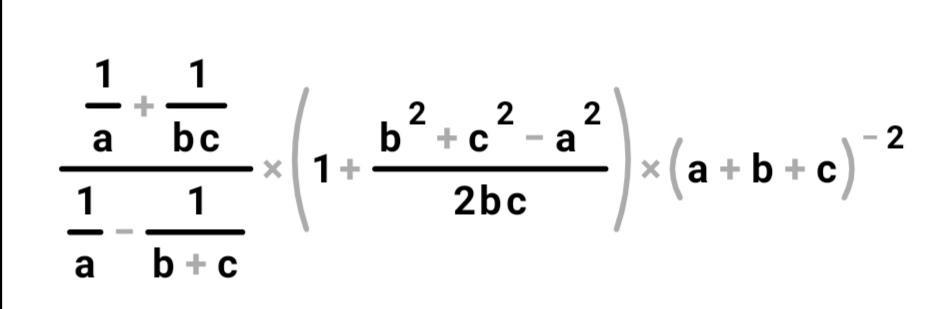
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: leramlera75
Предмет: Другие предметы,
автор: офыврблц
Предмет: География,
автор: ТвояМилая
Предмет: Геометрия,
автор: Аноним