Предмет: Геометрия,
автор: iradubrovina06
*ДАЮ 35 БАЛЛОВ!!!*
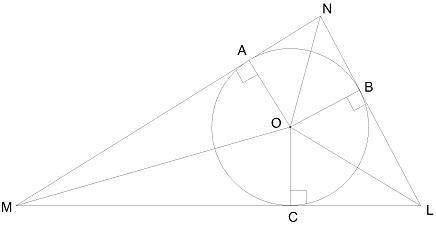
В треугольник вписана окружность. Вычисли неизвестные углы, если ∢ NMO = 26° и ∢ ONL = 29°.
∢ AOC = _°;
∢ AOB = _°;
∢ COB = _°.
Приложения:
siestarjoki:
Центр вписанной окружности - точка пересечения биссектрис.
OM - биссектриса, делит угол M пополам.
В четырехугольнике MAOC сумма противоположных углов 180.
а почему ты не напишешь это в ответе? тебе бы баллы достались
Ответы
Автор ответа:
2
Центр вписанной окружности O - точка пересечения биссектрис.
OM - биссектриса, делит угол M пополам.
∠M =2∠NMO =26° *2 =52°
В четырехугольнике MAOC сумма противоположных углов 180°, следовательно сумма двух других углов также 180°.
∠AOC =180°-∠M =180°-52° =128°
Аналогично ∠AOB =180°-(29° *2) =122°
∠COB =360°-∠AOC-∠AOB =110°
Похожие вопросы
Предмет: Английский язык,
автор: kostjaev1
Предмет: Английский язык,
автор: sekretabc
Предмет: Русский язык,
автор: Amina250878
Предмет: Алгебра,
автор: 0ло
Предмет: Математика,
автор: Maxsimmmka