Предмет: Алгебра,
автор: Арина261105
Решите способом введения новой переменной систему уравнений:
Приложения:
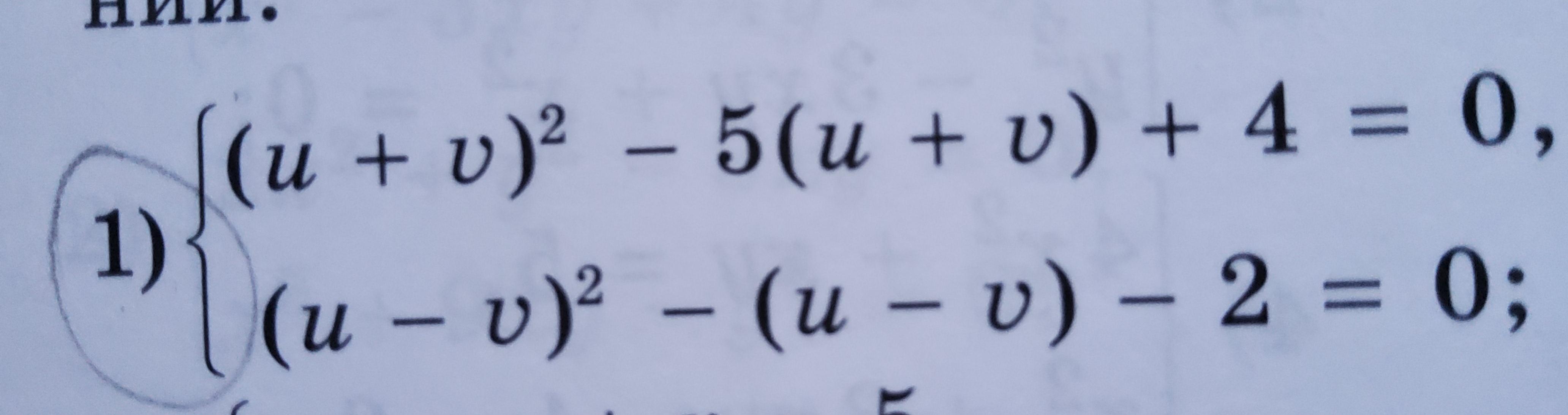
Ответы
Автор ответа:
4
Автор ответа:
4
Ответ:
Объяснение:
во вложении
Приложения:
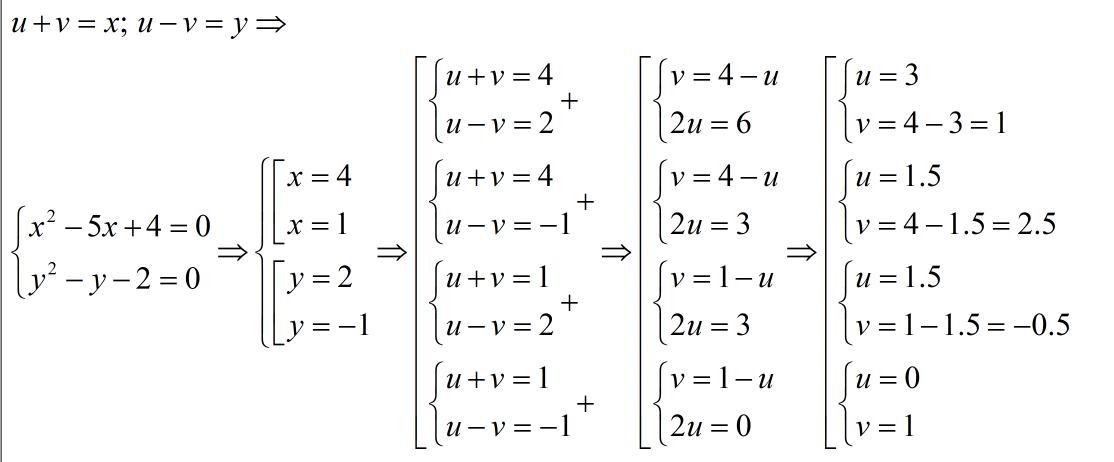
Похожие вопросы
Предмет: Английский язык,
автор: nastyushkakarg
Предмет: Английский язык,
автор: krybina71
Предмет: Английский язык,
автор: моrrrковка
Предмет: Химия,
автор: aidynzhumaghul
Предмет: Биология,
автор: alinaevseeva0