Question

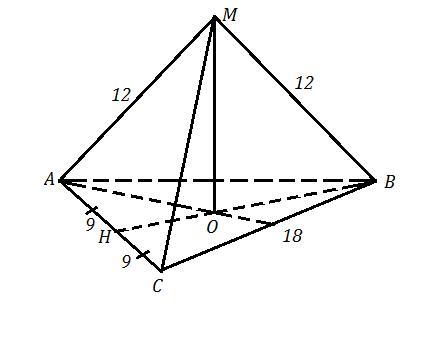
Треугольник ABC равносторонний со стороной, равной 18см. Точка М удалена от вершин треугольника на 12см. Найти расстояние отточки М до плоскости ABC.

Answer 1

Ответ:

Пошаговое объяснение:

ответ, с решением на этом изображении

448d75d0b56c8548d7da1151e447af81.docx

Answer 2

Ответ:  6 см .

Пошаговое объяснение:

ΔАВС , АВ=ВС=АС=18 см , АМ=ВМ=СМ=12 см , МО⊥АВС .  МО = ?

Высота ΔАВС равна   $BH=h=\sqrt{18^2-9^2}=\sqrt{243}$  .

Из ΔВОМ:

$MO=\sqrt{12^2-(\frac{2}{3}\cdot h)^2}=\sqrt{12^2-(\frac{2}{3}\cdot \sqrt{243})^2}=\sqrt{144-108} =\sqrt{36}=6$