Предмет: Алгебра,
автор: davidthanks83
Докажите что значение выражения положительное число
Приложения:
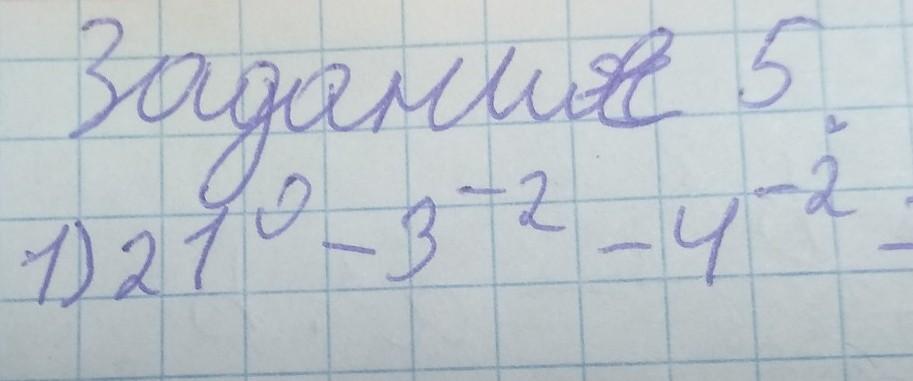
Ответы
Автор ответа:
6
Ответ:
Объяснение:
Посчитаем:
Тут выражение, равное разности степеней чисел 21 , 3 и 4
Свойство степени числа такое:
1. если показатель (цифра сверху) положительное (больше нуля), то пишем обычную степень .
2. если показатель равен нулю
3. если показатель меньше нуля, то пишем так:
Рассмотрим на нашем примере и посчитаем:
1) 21 в 0 степени - 1 по второму свойству.
2) 3 в степени -2 равно по 3 свойству.
3) 4 в степени -2 равно по 3 свойству.
А затем выполним над ними операции, приведя к общему знаменателю:
144, так как 144 делится и на 16, и на 9 , чтобы было удобнее считать.
- положительное число, то есть число. которое больше 0. Что и требовалось доказать.
davidthanks83:
а можешь объяснить ?
не панимаю что тут написано
спасибо
Похожие вопросы
Предмет: Русский язык,
автор: Улька2001ТыСупер
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: dsulin
Предмет: История,
автор: aminanik95
Предмет: Литература,
автор: GUNAY234