Предмет: Алгебра,
автор: CherryYT
65 баллов! Алгебра помогите система уравнкний
Приложения:
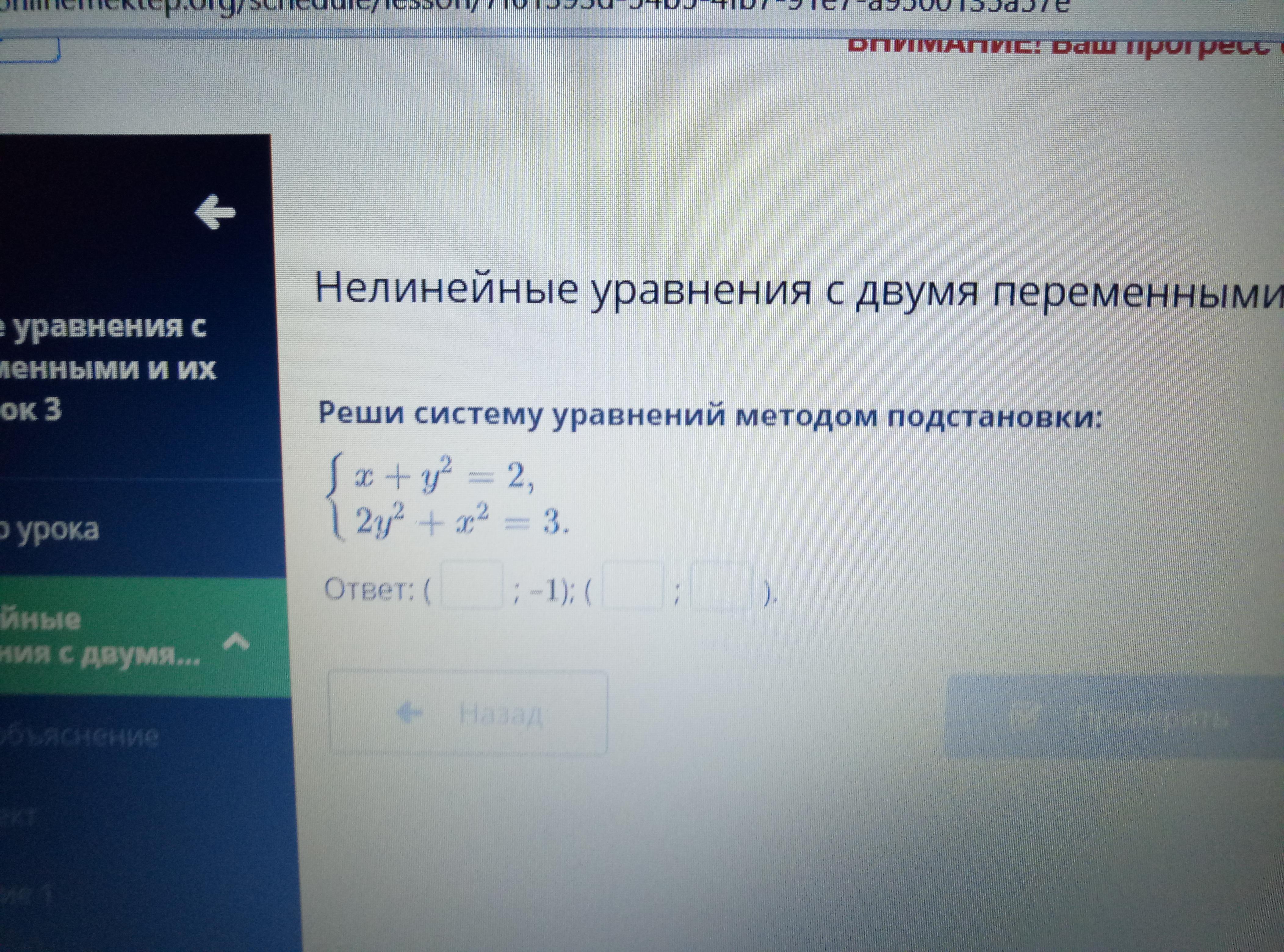
CherryYT:
Пж
Блин мало времени
Ответы
Автор ответа:
1
Ответ:
Всего, строго говоря, 2 пары значений:
(1;-1); (1;1)
Объяснение:
или
Это мы вместо у² записали (2-х)
Ну и решаем кватратное уравнение:
У квадр. уравнения только 1 корень: х=1
Из 1-го уравнения системы найдем у
и получаем :
х = 1
у = ±✓(2-1) = ±✓(1)
Причем стоит заметить, что одному найденному значению х соответствуют 2 варианта значения у
Т.е. всего, строго говоря, корней имеется 2 пары
Ответ: (1;-1); (1;1)
Спасибо большое
Стой
Не надо решать
Я понял
Не трать время
ага
Надо у в квадрате выразить через х
и подставить во второе уравнение
Посмотри, я исправился:). Так ведь вроде даже верно))
Топ
Автор ответа:
0
Ответ:
(1;1) , (1;-1)
Тогда
Имеем 2 пары:
Неверно
Похожие вопросы
Предмет: Русский язык,
автор: ПоБеДиТеДь
Предмет: Русский язык,
автор: 223354386
Предмет: Русский язык,
автор: luniov03
Предмет: Алгебра,
автор: Екатерина015
Предмет: Математика,
автор: duharulitAxx2000