Question

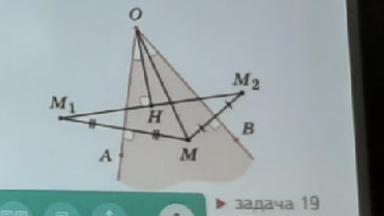
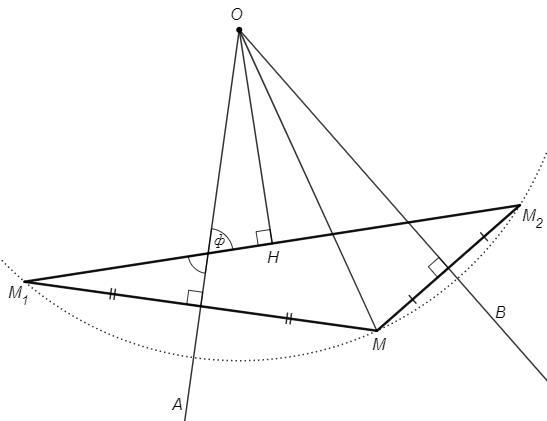
Точку М, лежащую внутри острого угла АОВ, симметрично отразили относительно его сторон и получили точки М1 и М2 (см. рисунок). На отрезок М1М2 из точки О опустили перпендикуляр ОН. Докажите, что углы АОН и ВОМ равны.

Answer 1

AO, BO - серединные перпендикуляры к сторонам △MM1M2, следовательно точка пересечения O является центром описанной окружности △MM1M2.

AOH =90-ф =M1 =∪MM2/2

Перпендикуляр из центра делит хорду и стягиваемую дугу пополам.

BOM =∪MM2/2 => AOH=BOM