Предмет: Алгебра,
автор: ArtZETds
помогите решить пример
Приложения:
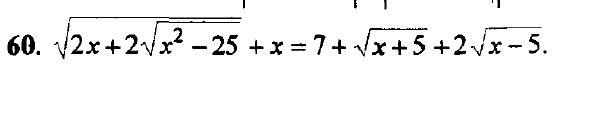
Ответы
Автор ответа:
1
Ответ:
Объяснение:
ArtZETds:
а почему вы раскрыли модуль только со знаком + ??
Сумма радикалов число всегда положительное
*Вернее неотрицательное
Вот если бы там был - между корнями, вот тогда уже не факт, нужно было бы раскрвывать
понял, спасибо большое
Похожие вопросы
Предмет: Русский язык,
автор: nastuhastic
Предмет: Английский язык,
автор: Alissium
Предмет: Русский язык,
автор: abdidov1
Предмет: Физика,
автор: kolyakrasnov8