Предмет: Математика,
автор: ventoauureo
Срочно! Помогите, пожалуйста решить задание. 35 баллов! Решить нужно то, что выделено, и как в примере
Приложения:
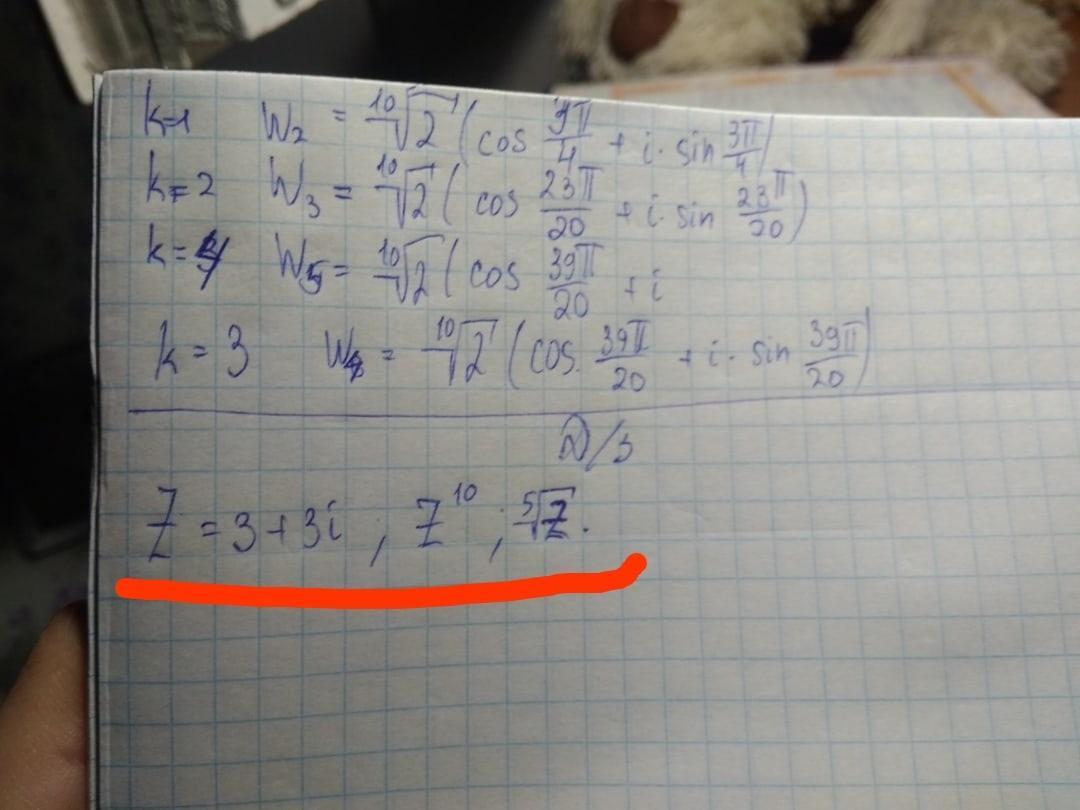
Ответы
Автор ответа:
0
Формулы Муавра:
Похожие вопросы
Предмет: Русский язык,
автор: katy2002top
Предмет: Русский язык,
автор: Bobodjonova2014
Предмет: Русский язык,
автор: Полик2005
Предмет: Физика,
автор: неумница1
Предмет: Математика,
автор: msromanenko199