Предмет: Математика,
автор: liza2829
Помогите решить систему методом Гаусса
Приложения:
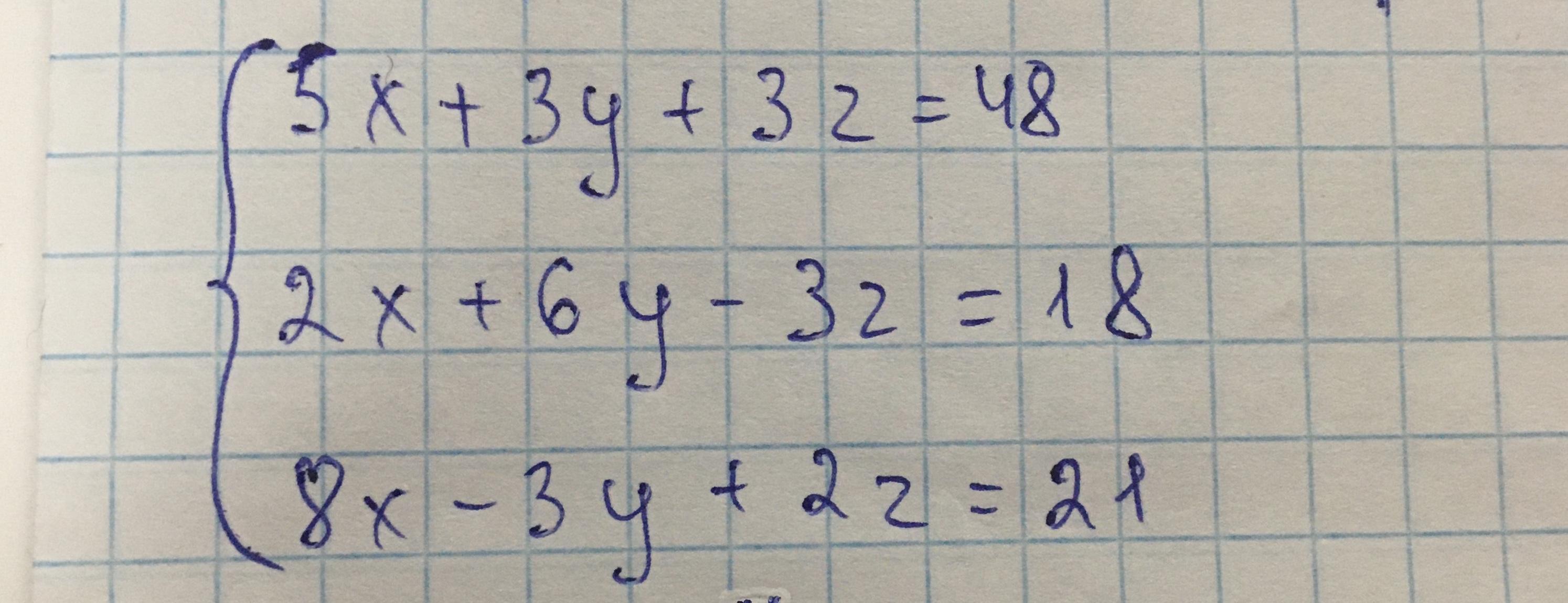
Ответы
Автор ответа:
0
Вычисляем определитель матрицы 3×3:
∆ =
5 3 3
2 6 -3
8 -3 2
= 5·6·2 + 3·(-3)·8 + 3·2·(-3) - 3·6·8 - 5·(-3)·(-3) - 3·2·2 = 60 - 72 - 18 - 144 - 45 - 12 = -231.
Находим определители:
∆1 =
48 3 3
18 6 -3
21 -3 2
= 48·6·2 + 3·(-3)·21 + 3·18·(-3) - 3·6·21 - 48·(-3)·(-3) - 3·18·2 = 576 - 189 - 162 -
- 378 - 432 - 108 = -693.
∆2 =
5 48 3
2 18 -3
8 21 2
= 5·18·2 + 48·(-3)·8 + 3·2·21 - 3·18·8 - 5·(-3)·21 - 48·2·2 = 180 - 1152 + 126 - 432 + 315 - 192 = -1155.
∆3 =
5 3 48
2 6 18
8 -3 21
= 5·6·21 + 3·18·8 + 48·2·(-3) - 48·6·8 - 5·18·(-3) - 3·2·21 = 630 + 432 - 288 - 2304 + 270 - 126 = -1386.
Ответ:
x = ∆1 / ∆ = -693 / -231 = 3.
y = ∆2 / ∆ = -1155 / -231 = 5.
z = ∆3 / ∆ = -1386 / -231 = 6.
Похожие вопросы
Предмет: Русский язык,
автор: nastya22067
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: kyltisheva79
Предмет: Математика,
автор: влад20084
Предмет: Математика,
автор: iralina009