Предмет: Алгебра,
автор: Noname3890000
Можно, пожалуйста, решение номера 70 пункты В и Е. Нужно воспользоваться одной из 6 формул. Даю 20 баллов.
Приложения:

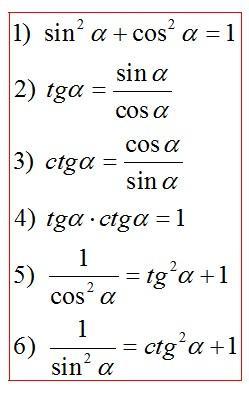
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Другие предметы,
автор: SaintInquisition
Предмет: Русский язык,
автор: Diok2015
Предмет: Другие предметы,
автор: yanasirik
Предмет: Математика,
автор: Голубиная
Предмет: ОБЖ,
автор: аНяБоДрОвА