Question

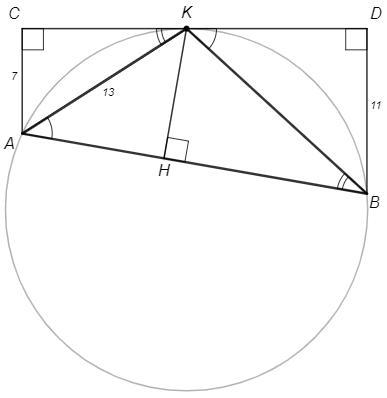
Прямая L касается окружности в точке K. На окружности выбраны точки A и B, лежащие по разные стороны от диаметра, проходящего через точку К. Найдите площадь треугольника AKB, если расстояния от точек A и B до прямой l равны соответственно 7 и 11, а AK=13. Ответ округлите до целого числа.

Answer 1

DKB =∪KB/2 =KAB (угол между касательной и хордой)

CKA =∪KA/2 =KBA

△KAH~△BKD, AK/BK =KH/BD

△KBH~△AKC, BK/AK =KH/AC

KH/BD=AC/KH => KH=√(AC*BD)=√77

BK =AK*KH/AC =13*√(11/7)

По теореме Пифагора

AH =√(AK^2 -KH^2) =√(13^2 -77) =√92

BH =√(BK^2 -KH^2) =√(13^2 -7^2)*√(11/7) =√120*√(11/7)

S(AKB) =1/2 (AH+BH) KH =1/2 (√92 +√120*√11/√7)*√77 =√23*√77 +11√30

Ответ: 102