Предмет: Геометрия,
автор: yasminacamilla
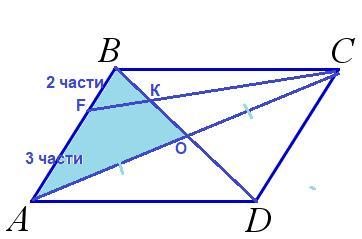
В параллелограмме ABCD на стороне AB отмечена точка F так, что AF : FB = 3 : 2. В каком отношении прямая CF делит диагональ BD?
Ответы
Автор ответа:
1
В параллелограмме ABCD на стороне AB отмечена точка F так, что AF : FB = 3 : 2. В каком отношении прямая CF делит диагональ BD?
Объяснение:
Пусть ВD пересекается с СF в точке К .Проведем диагональ АС. Диагонали точкой пересечения О разделятся пополам : АО=ОС.
По т. Менелая для ΔАВО или учитывая , что АС=2СО ,
,
. Значит на половину диагонали ВD приходится 7 частей ⇒ на всю ВD приходится 14 частей.. Тогда на отрезок КD=14-4=10 частей.
.
Приложения:
yasminacamilla:
Спасибо огромное!!!
Похожие вопросы
Предмет: Қазақ тiлi,
автор: GamoraХД
Предмет: Русский язык,
автор: svetlananestere
Предмет: Русский язык,
автор: likav12
Предмет: Химия,
автор: зайка1238
Предмет: Математика,
автор: дама000