Предмет: Геометрия,
автор: Аноним
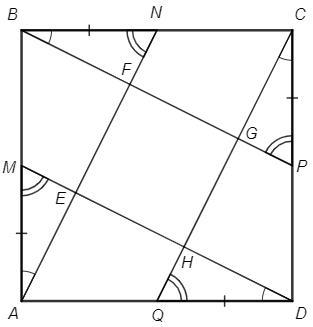
Точки M, N, P, Q — середины сторон AB, BC, CD, DA квадрата ABCD соответственно. Докажите, что точки пересечения прямых AN, BP, CQ, DM являются вершинами квадрата
Ответы
Автор ответа:
1
△ABN=△BCP=△CDQ=△DAM (по двум катетам) => соответствующие стороны и углы равны
△MAE=△NBF=△PCG=△QDH (по стороне и прилежащим углам)
Вычитая из равных отрезков равные, выясняем, что EFGH - ромб.
(AN=BP, AE=BF, FN=GP ... => AN-AE-FN =BP-BF-GP ... => EF=FG=GH=HE)
В △AME сумма острых углов 90 => E=90
EFGH - ромб с прямым углом, то есть квадрат.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: anya210893
Предмет: Другие предметы,
автор: zacelyuliya68
Предмет: Қазақ тiлi,
автор: аягозочка
Предмет: Математика,
автор: валентин3456
Предмет: Математика,
автор: alenka6776