Предмет: Геометрия,
автор: Minikoshechca555
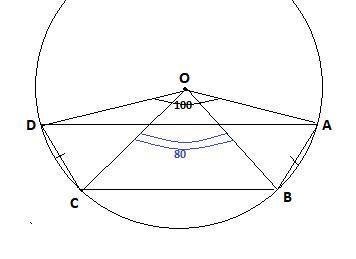
Трапеция ABCD с основанием AD вписана в окружность с центром О.Найдите углы трапеции,если ∠AOD=100°,∠BOC=80° и точка О лежит вне трапеции.
Ответы
Автор ответа:
1
Трапеция ABCD с основанием AD вписана в окружность с центром О.Найдите углы трапеции,если ∠AOD=100°,∠BOC=80° и точка О лежит вне трапеции.
Объяснение:
Вписанная в окружность трапеция является равнобедренной.
Значит АВ=CD стягивают равные дуги → ∪AB=∪CD
∠BOC=80° -центральный → ∪ВС=80°
∠AOD=100°--центральный → ∪АВD=100° ⇒ ∪AB=∪CD= =10°.
∠BAD вписанный и опирается на дугу ∪BCD=∪BC+∪CD=80°+10°=90°.
∠BAD=1/2*90°=45°. Значит ∠СDA=45° и ∠СВA=45° (углы при основании равны )
Сумма углов 4-х угольника 360°. Поэтому ∠АВС=∠ВСD= =135°
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: ironman48
Предмет: Английский язык,
автор: VLADIOROM
Предмет: Русский язык,
автор: vikiars
Предмет: Математика,
автор: ZRMaxMud
Предмет: Математика,
автор: sonya364