Предмет: Алгебра,
автор: veronika050343
помогите решить уравнение
Приложения:
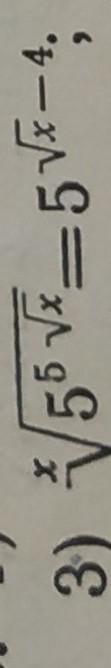
Ответы
Автор ответа:
1
Ответ:
х=25
Объяснение:
записываем уравнение в виде степени с основанием 5, используя выражение
т. к. основания одинаковы, нужно приравнять показатели
упрощаем выражение, сократив х и в дроби, получаем:
решаем уравнение методом замены переменной, вместо подставляем t, получаем:
решаем уравнение
t₁=-1
t₂=5
подставляем значения
=-1
=5
решаем получившиеся уравнения
х₁=∅ (решения нет)
х₂= 25
Ответ: 25
Похожие вопросы
Предмет: Английский язык,
автор: Renaata
Предмет: Английский язык,
автор: Margo310
Предмет: Українська мова,
автор: gordienkonik
Предмет: Алгебра,
автор: DimkMix
Предмет: Химия,
автор: ruziev883