Предмет: Алгебра,
автор: crezy221220
Найти производную! Помогите
Приложения:
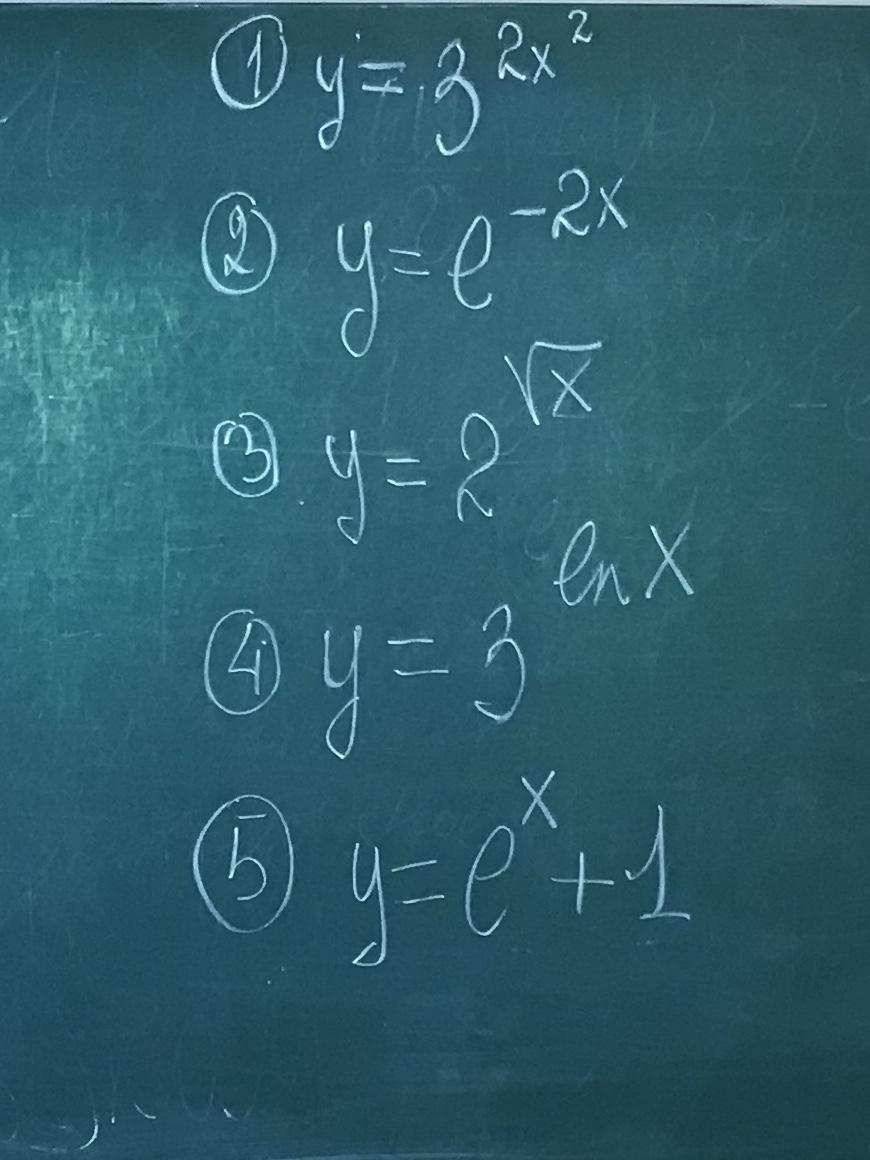
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: smirnovamama
Предмет: Русский язык,
автор: dilarah
Предмет: Русский язык,
автор: andreevaelizave
Предмет: Математика,
автор: 9507896
Предмет: Математика,
автор: Alinazz05