Предмет: Геометрия,
автор: welrony
Стороны треугольник равны 6, 8, 10. К стороне проведена биссектриса. Найди длины отрезков, на которые она делит эту сторону
Iife20:
К какой именно стороне проведена биссектриса?
К большей*
спасибо
может к стороне 8см? там ответ целый получается
Написано, к большей стороне
Ок
Ответы
Автор ответа:
0
Ответ:
АК=30/7, СК=40/7
Объяснение:
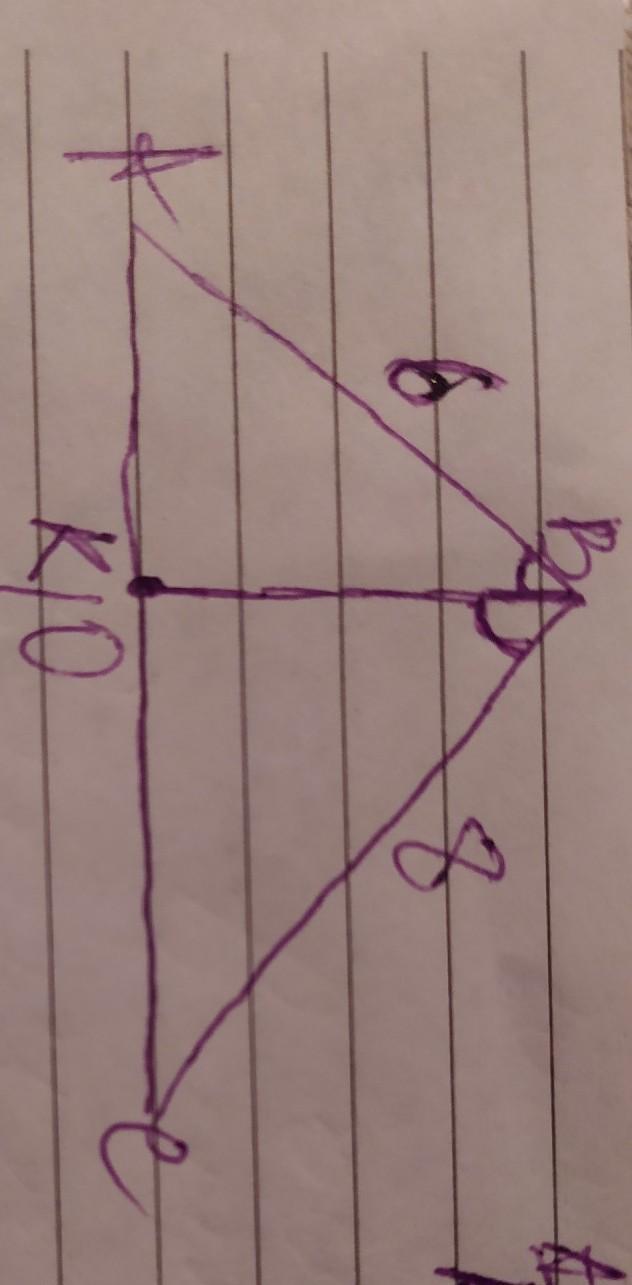
обозначим вершины треугольника А В С с биссектрисой ВК. Биссектриса угла делит противоположную сторону на отрезки пропорционально прилежащим сторонам, поэтому
обозначим эти пропорции как 3х и 4х и зная величину стороны составим уравнение:
3х+4х=10
7х=10
х=10/7
Тогда АК=
СК=
проверка: 40/7+30/7=70/7=10см
если бы биссектриса была проведена к стороне 8, тогда соотношение отрезков этой стороны было бы как 6/10=3/5, и тогда обозначаем пропорции 3х и 5х и составляем такое уравнение:
3х+5х=8
8х=8
х=8÷8=1
тогда одна часть отрезка=3×1=3см, а вторая=5×1=5см
Отрезки: 3см и 5см
посмотри, может в задании опечатка и если этот вариант правильный, то запишите его
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Ekaterina8583
Предмет: Українська мова,
автор: ILoveYouBOG
Предмет: Русский язык,
автор: kanaikinae
Предмет: Литература,
автор: Alinoh
Предмет: Математика,
автор: даша2832