помогите пожалуйста
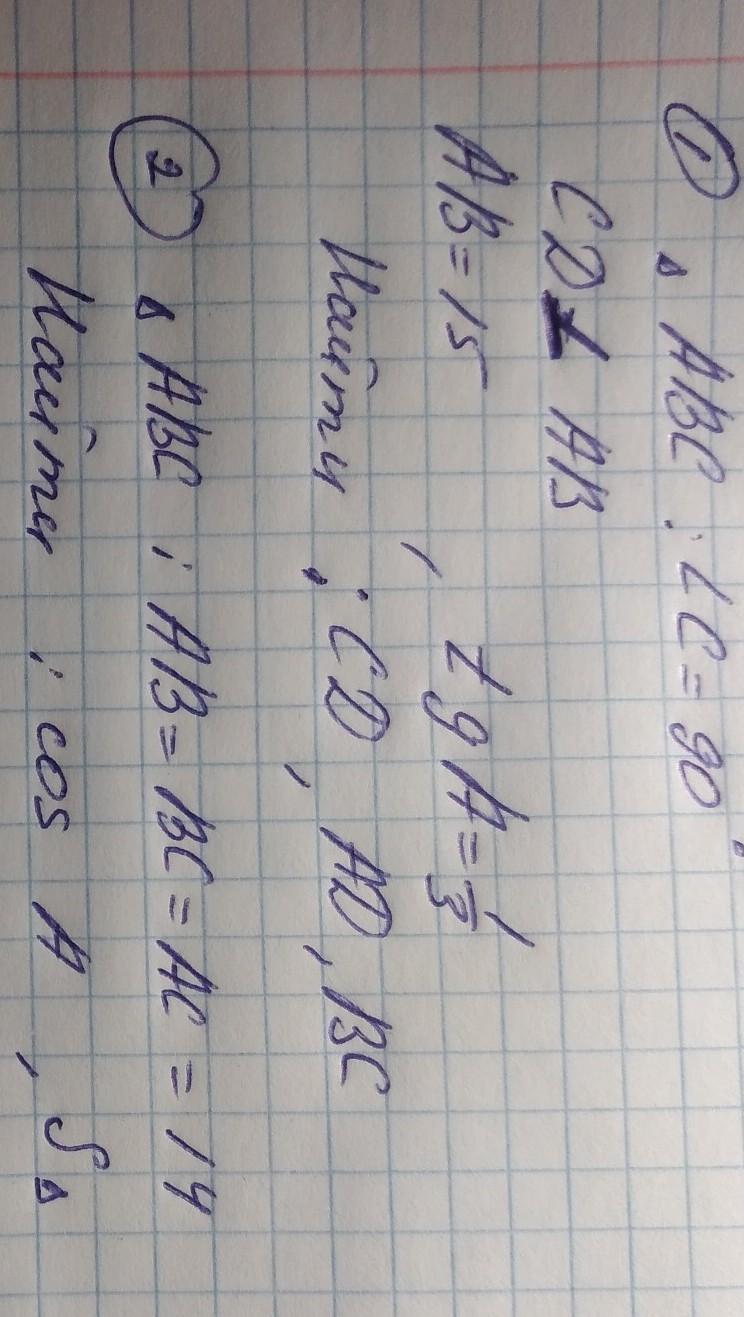
Ответы
1) В данной задаче мы работаем с прямоугольным треугольником. Тангенс - это отношение противолежащей стороны к прилежащей.
Из данной пропорции можно сделать вывод, что ВС = х, а АС = 3х
По т. Пифагора:
х²+(3х)²=15²
10х² = 225
х² = 22,5
х = √22,5
Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключённого между катетом и высотой, проведённой из вершины прямого угла
BC²=BD*AB
BD = BC² : AB
BD = 22,5 : 15
BD = 1,5
AD = AB - BD = 15 - 1,5 = 13,5
Высота, проведённой из вершины прямого угла, прямоугольного треугольника есть среднее пропорциональное для отрезков, на которые делится гипотенузы этой высотой.
CD=√(BD*AD)
CD=√(1,5*13,5)
CD=√20,25
CD = 4,5
Ответ: CD = 4,5; AD = 13,5 ; ВС = √22,5
2) а)По условию нам известно, что все стороны равны ⇒треугольник равносторонний. У равностороннего треугольника все углы равны по 60°. Как известно:
Или же:
Высота проведённая в равнобедренном или равностороннем треугольнике является также её биссектрисой и медианой. Получается что основание делится на 2, то есть 14:2=7. Рассмотрим один из полученных прямоугольных треугольников. Косинус это отношение прилежащей стороны к гипотенузе.
б)
Или же:
Т.к. высота разделила наш равносторонний треугольник на 2 прямоугольных то:
По т. Пифагора:
h = √(14²-7²)
h = √(196-49)
h = √147
h = 7√3
Ответ: cos A = 0,5 ; SΔ = 49√3
https://znanija.com/task/38092249
1) Дано: ∠C=90°; CD ⊥AB ; AB=15 ; tgA =1/3
- - - - CD -? , AD -? BC -?
2) Дано: AB = BC = AC = 14 - - - - cosA - ? , S= S( ΔABC) -?
Ответ: 1) 4,5 ; 12,5 ; 1,5√10 ;
2) 1/2 ; 49√3 .
Объяснение: 1) cos²A + sin²A = 1 || : cos²A
1 +tg²A = 1/cos²A ⇒ cos²A= 1/√(1 +tg²A)
cosA = 1/√(1+tg²A) = 1 /√(1+ (1/3)²) = 3/√10. || ∠A < 90° ||
SinA = tgA*cosA = tgA/√(1+tg²A) = (1/3)* (3/√10) = 1/√10
AC = AB*cosA =15*3/√10 =15*3*√10/10 =3*3√10 /2 = 4,5√10 ;
AD =AC*cosA=4,5√10 *3 /√10 = 12,5 * * * из ΔADC * * *
BC = AB*sinA =15*1/√10 =15*√10 / 10 = 1,5 √10 ;
S(ABC) =AB*CD/2 =AC*BC/2 ⇒
CD =AC*BC/AB=4,5√10*1,5√10 /15 =4,5
- - - - - -
2)
cosA =cos60° = 1/2 ; sinA =sin60° = √3/2 || sinA =√(1 - cos²A) ||
S =(1/2)a*h = (1/2)a*√(a² -(a/2)² ) = a²√3 /4 = 14²√3 / 2²=7²√3 =49√3
S =( 1/2)a*a*sin60° = a²√3 /4
По формуле Герона :
S =√p(p-a)(p -b)(p-c) , где p =(a+b+c)/2 → полупериметр Ф
S=√( (3a/2) *(a/2)*(a/2)*(a/2) ) = a²√3 /4
* * * * * * * * * * * * * * * * * * * * * см еще и приложение
