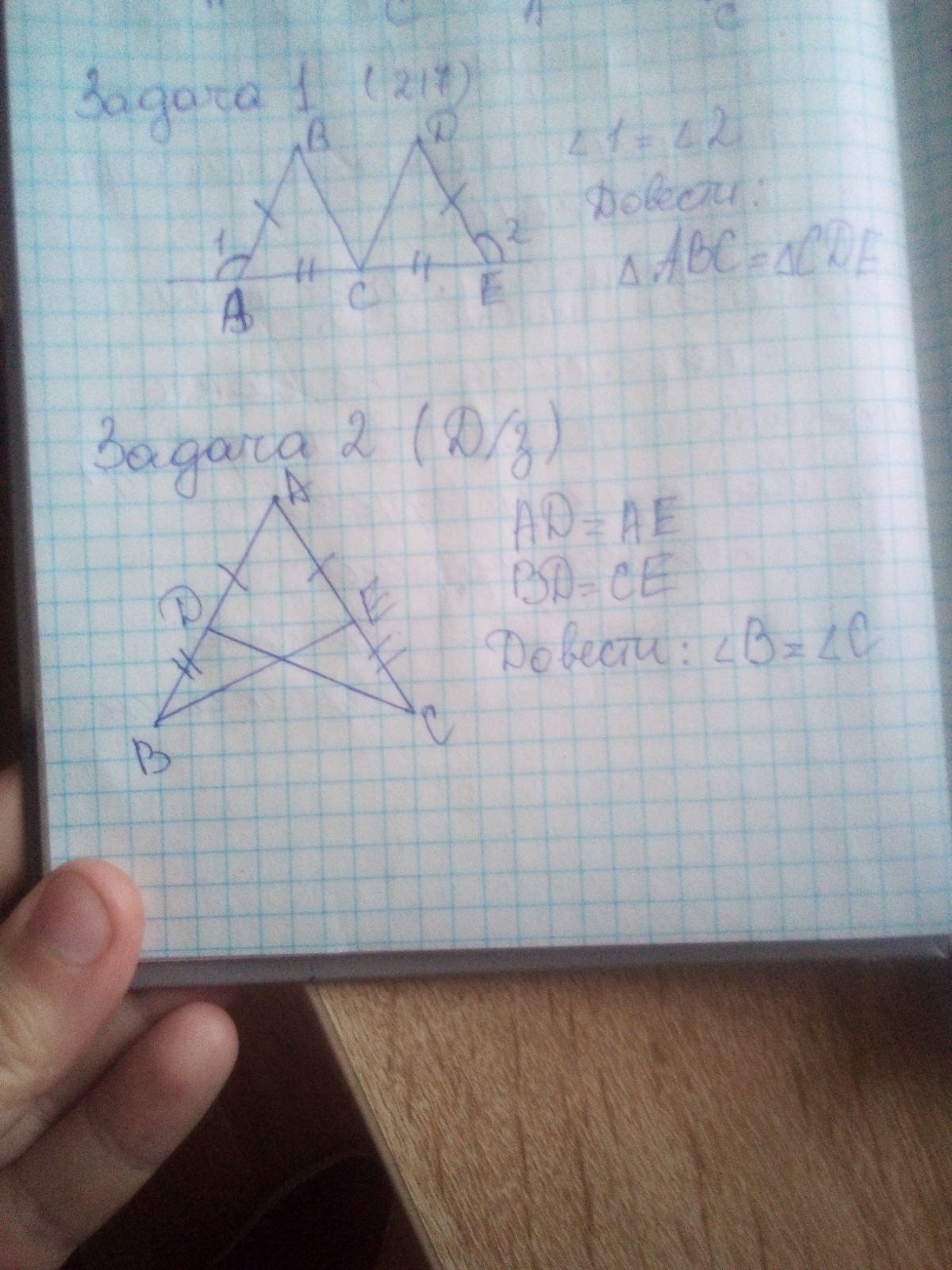
помогите пожалуста решыть 2 задачу
Ответы
Когда идет речь о доказательстве равенства углов в треугольниках, то, скорее всего, намекают на признаки равенства треугольников. Ведь если мы докажем равенство треугольников, работать будет с ними гораздо приятнее.
Вспомним признаки равенства треугольников:
1. По двум сторонам и углу между ними.
2. По стороне и двум прилежащим углам.
3. По трём сторонам.
Теперь возвращается к рисунку, а, конкретнее, к треугольникам ВЕА и СDА.
Понятное дело, признак №3 нам точно не подходит... Равенство дано только одной пары сторон. Признак №2 сразу отпадает... Про какие-то углы речи не идёт вообще. А вот... Признак №1 рассмотреть стоит. Что нужно для его действия? Две равных стороны и угол. Пошлите собирать)
Если обратить внимание на положение треугольников, то можно заметить, что верхний угол А принадлежит как треугольнику ВЕА, так и треугольнику СDА. Соответственно, равный угол мы нашли. Дальше нужно две стороны. Смотрим. По условию, DA=AE. Это уже равенство одной пары сторон. Теперь нужна последняя - третья пара. Обратим внимание на чертёж, заметим, что если BD=СЕ и DA=EA, то и ВА=СА (BD+DA=BA, CE+EA=CA).
Что мы нашли? Угол А (сверху) - общий, стороны АD и АЕ равны, стороны АВ и АС равны. Делаем вывод:
Треугольники ВАЕ и САD равны по первому признаку равенства треугольников. Значит, их соответственные элементы равны.
Угол В и угол С - соответственные элементы в треугольниках.
Угол В=С, ч.и.т.д.